Journal Exercices de programmation et benchmarks

Posté par  (site web personnel) . Licence CC By‑SA.
Étiquettes :
48
11
fév.
2020

Sommaire

Bonjour 'nal,

Un petit exercice d'algorithmique m'a récemment poussé à regarder en détail l'impact de différentes approches sur les performances et à remettre en question des connaissances que je croyais solides. Laisse-moi te raconter ce voyage.

Pour être en bonne santé, exercez-vous régulièrement

J'aime bien pratiquer des exercices de programmation sur des sites tels que CodinGame ou CodeSignal. Si tu ne connais pas, ces sites proposent un petit IDE en ligne et divers problèmes d'algorithmiques avec jeux de tests associés. Le jeu consiste à fournir dans l'éditeur en ligne un programme pour résoudre le problème donné ; l'implémentation se faisant dans le langage de ton choix. La plate-forme permet de lancer la solution sur les jeux de tests pour la valider.

Selon son profil on utilisera le service dans l'optique d'écrire le programme le plus court, ou le plus efficace, ou simplement un programme qui fonctionne. Pour moi c'est un peu un coding dojo : un lieu ou pratiquer et où se comparer aux autres pour apprendre et s'améliorer.

En particulier, lors d'une séance sur CodeSignal je me suis laissé allé à me comparer à la meilleure solution d'après les votants : pour chaque exercice j'implémente une solution d'une manière assez immédiate, un peu comme ça me vient, puis quand la solution est validée je regarde celles des autres. J'essaye de trouver leurs points forts, les miens, et je nous critique. Comme je fais les exercices en C++ je ne me compare qu'à la meilleure solution dans ce langage.

Présentation de l'exercice

Étant donné une matrice d'entiers, l'exercice consiste à calculer la somme des nombres qui ne sont pas sous un zéro. Par exemple, pour

0, 2, 3
1, 0, 4
5, 6, 7

Le résultat attendu est 2 + 3 + 4 + 7 = 16. Le 1, le 5 et le 6 ne sont pas comptés car il y a un zéro plus haut dans la colonne.

La matrice est représentée en row-major, c’est-à-dire par une table de tables où chaque sous table représente une ligne de la matrice. J'ai déjà rencontré des traitements de grandes matrices par le passé et ma première réflexion est « si je traite le problème par colonne comme le suggère l'énoncé je vais sauter d'une zone mémoire à une autre et avoir des perfs nases. Il vaut mieux traiter ce genre de matrice ligne par ligne. »

Je vais donc scanner les lignes pour additionner les valeurs. Un booléen associé à chaque colonne me dira si j'ai déjà rencontré un zéro dans cette colonne, auquel cas j'ignore la valeur.

En pratique je vais donc visiter des cases pour lesquelles je sais que les valeurs seront ignorées, que je n'aurais pas visitées en scannant par colonne, mais pour l'instant je pense que c'est pour le mieux.

De plus, peu avant de faire l'exercice j'avais visionné les présentations Parsing JSON Really Quickly: Lessons Learned (Daniel Lemire), Speed Is Found In The Minds of People (Andrei Alexandrescu) et Path Tracing Three Ways: A Study of C++ Style (Matt Godbolt) dans lesquelles les auteurs avaient amélioré les performances de manière remarquable en implémentant leurs algorithmes de manière branchless, c’est-à-dire sans conditions if qui amènent le prédicteur du processeur à faire des suppositions. Sans entrer dans les détails, il faut savoir qu'une prédiction a un coût d'annulation parfois plus grand que ce qui a été gagné par les prédictions justes. Un code sans conditions évite ce problème et se comporte de manière stable, mais il faut réussir à intégrer quelque chose correspondant à la condition dans les calculs.

Implémentation initiale

Assez de bla bla, allons dans le code. L'implémentation initiale (que tu peux retrouver dans ce dépôt sur GitHub) ressemble à cela :

int matrix_elements_sum_branchless(const std::vector<std::vector<int>>& matrix)
{
  const int row_size(matrix[0].size());
  std::vector<char> usable_column(row_size, 1);

  int result(0);

  for (const std::vector<int>& row : matrix)
    for (int i(0); i != row_size; ++i)
      {
        const int v(row[i]);
        result += v * usable_column[i];
        usable_column[i] *= (v != 0);
      }

  return result;
}

Il n'y a pas beaucoup de lignes mais déjà beaucoup de questions, à commencer par « est-ce que c'est vraiment mieux qu'un scan de colonnes ? ». Regardons donc la solution la mieux notée sur CodeSignal.

int matrix_elements_sum_best_ratings(const std::vector<std::vector<int>>& m)
{
  int r(0);

  for (int j=0; j<(int)m[0].size(); j++)
    for (int i=0; i<(int)m.size(); i++)
      {
        if (m[i][j]==0)
          break;
        r += m[i][j];
      }

  return r;
}

Bien, ça m'a l'air d'être un scan de colonnes justement ! Comparons les performances des deux implémentations à l'aide de Google Benchmark.

Le jugement

Pour les tests j'utilise une matrice de valeurs aléatoires, chaque cellule ayant une chance d'autant plus grande d'être zéro qu'elle est proche du bas de la matrice. Bien que l'énoncé indiquait une taille maximum de 10×10 pour la matrice, je teste aussi pour des tailles supérieures : 100×100, 1000×1000 et 10000×10000.

Run on (4 X 3100 MHz CPU s)
CPU Caches:
  L1 Data 32 KiB (x2)
  L1 Instruction 32 KiB (x2)
  L2 Unified 256 KiB (x2)
  L3 Unified 3072 KiB (x1)
-------------------------------------------------------------
Benchmark                   Time             CPU   Iterations
-------------------------------------------------------------
branchless/10             147 ns          147 ns      4624304
branchless/100          13613 ns        13612 ns        50630
branchless/1000       1363899 ns      1363210 ns          516
branchless/10000    134339389 ns    134330069 ns            5
best_ratings/10          40.5 ns         40.5 ns     17268039
best_ratings/100         1422 ns         1422 ns       485581
best_ratings/1000       49662 ns        49662 ns        14096
best_ratings/10000    3599890 ns      3599673 ns          204

Wow, la version la mieux notée est bien meilleure de la mienne ! Voyons si je peux améliorer ça. Déjà je me demande si l'implémentation branchless est vraiment mieux qu'une version avec branches. Comparons avec cette implémentation :

int matrix_elements_sum_branches(const std::vector<std::vector<int>>& matrix)
{
  const int row_size(matrix[0].size());
  std::vector<char> usable_column(row_size, 1);

  int result(0);

  for (const std::vector<int>& row : matrix)
    for (int i(0); i != row_size; ++i)
      if (usable_column[i])
        {
          const int v(row[i]);

          if (v == 0)
            usable_column[i] = 0;
          else
            result += v;
      }

  return result;
}

Nouveaux résultats :

-------------------------------------------------------------
Benchmark                   Time             CPU   Iterations
-------------------------------------------------------------
branchless/10             161 ns          161 ns      4315630
branchless/100          13757 ns        13757 ns        46364
branchless/1000       1352468 ns      1352375 ns          517
branchless/10000    134475422 ns    134475261 ns            5
branches/10               116 ns          116 ns      5764899
branches/100             7689 ns         7689 ns        84635
branches/1000          781502 ns       781443 ns          861
branches/10000       70365787 ns     70364814 ns            8
best_ratings/10          42.0 ns         42.0 ns     16691501
best_ratings/100         1091 ns         1091 ns       628554
best_ratings/1000       41888 ns        41886 ns        16697
best_ratings/10000    3454331 ns      3454125 ns          203

Mmmmh okay, donc la version branchless se comporte moins bien que la version avec branches. Décidémment c'est mal parti.

Des benchmarks et trop d'idées

Tiens, j'ai envie de tester avec un std::vector<bool> pour usable_column. Je doute que ça apporte un réel gain mais je me demande quel impact aurait l'implémentation bitset par rapport à la précédente. Ça commence à faire beaucoup de lignes dans l'output alors passons en mode graphique et profitons-en pour ajouter des tailles de matrices.

Apparemment mon ordinateur a un cache L1 de 32 ko, deux caches L2 de 256 ko et un cache L3 de 3072 ko. Cela signifie que sur des entiers de 32 bits les matrices en dessous de 64×64 tiennent dans un cache L1, puis dans L2 jusqu'à 128×128, puis L3 jusqu'à 512×512. Au delà il faudra aller chercher les données en RAM.

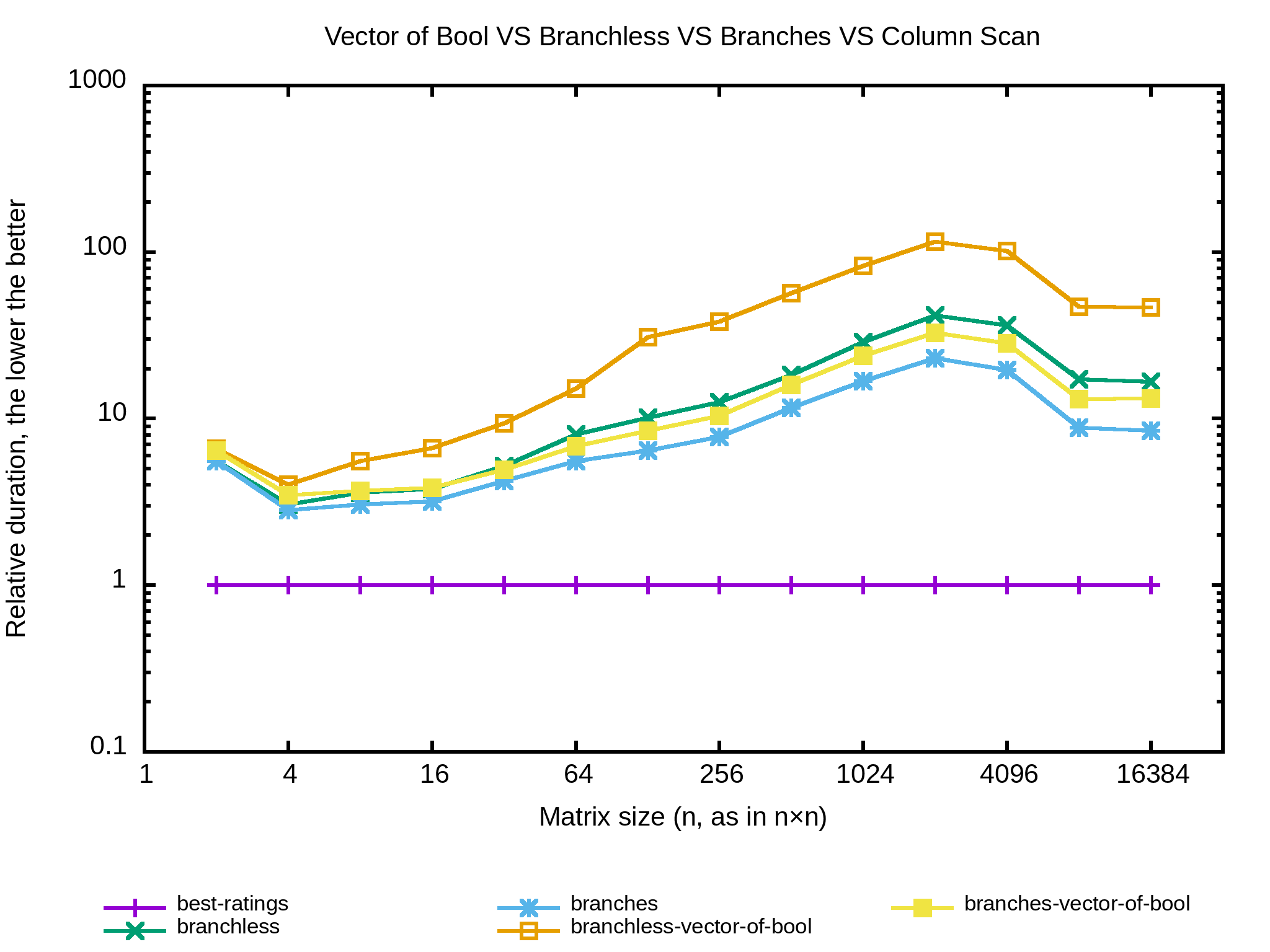
Bien, bien, bien… Les implémentations qui utilisent un std::vector<bool> sont moins efficaces que les originales, et dans tous les cas c'est pire que la version en colonnes.

Et si je stockais les indices de la première et la dernière colonne encore pertinentes ? Ainsi le nombre de colonnes scannées devrait réduire au fur et à mesure que l'on descend dans la matrice. Ça donne quelque chose comme ça :

int matrix_elements_sum_branches_range
(const std::vector<std::vector<int>>& matrix)
{
  const int row_size(matrix[0].size());
  std::vector<char> usable_column(row_size, 1);

  int first(0);
  int last(row_size);
  int result(0);

  for (const std::vector<int>& row : matrix)
    {
      for (; (first != last)
             && ((usable_column[first] == 0) || (row[first] == 0));
           ++first);

      int last_non_zero(first);

      for (int i(first); i != last; ++i)
        if (usable_column[i])
          {
            const int v(row[i]);

            if (v == 0)
              usable_column[i] = 0;
            else
              {
                result += v;
                last_non_zero = i;
              }
          }

      last = last_non_zero + 1;
    }

  return result;
}

Et le benchmark :

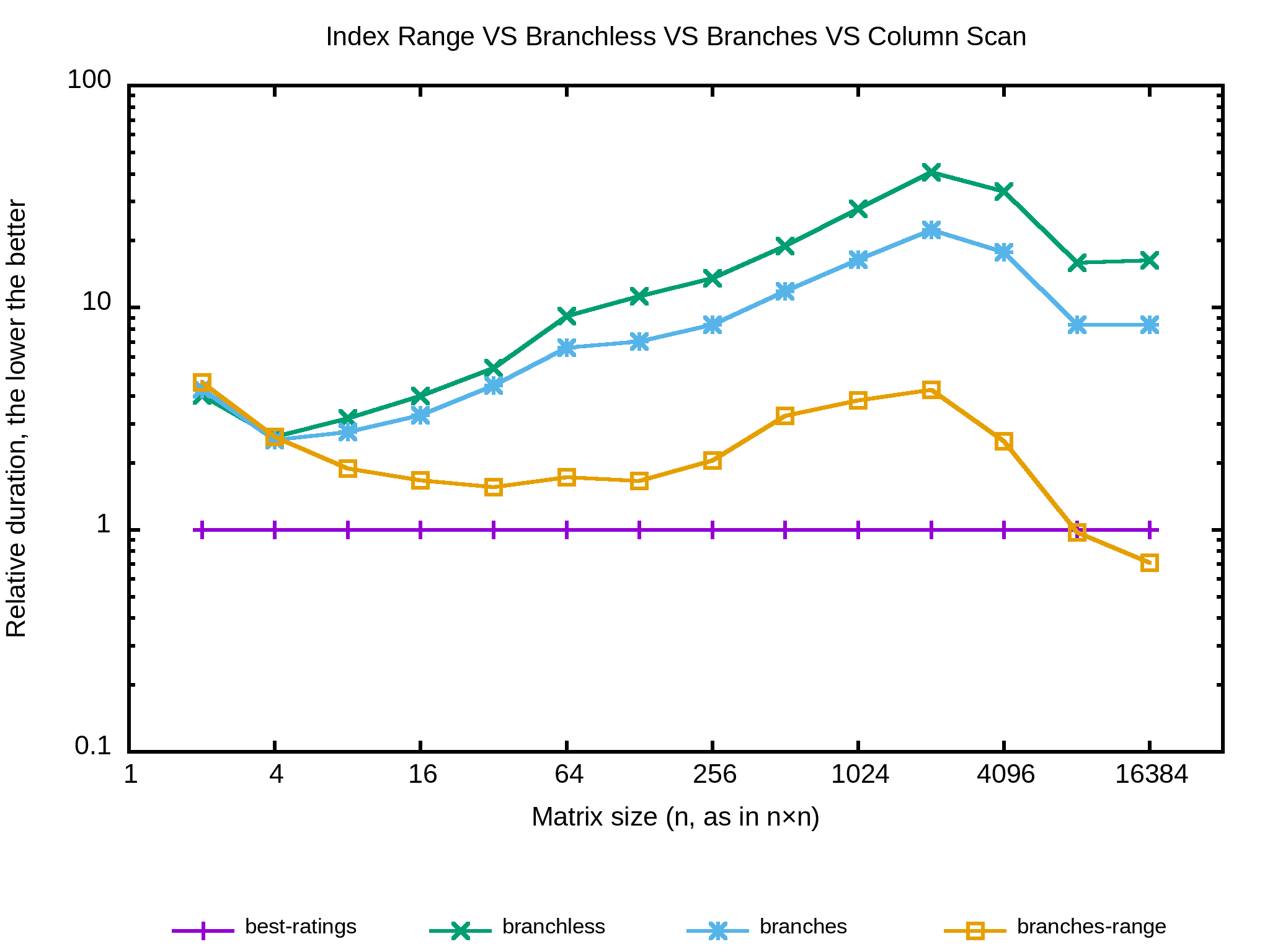
Ha-HA ! Ça coupe enfin la ligne de l'algo naïf. Est-ce qu'il y a moyen de faire mieux ? Déjà l'approche est un peu limite car l'intervalle des colonnes ne réduit efficacement que si les extrêmes contiennent des zéros assez haut. Je vais tenter de n'itérer que sur les colonnes dont je sais qu'elles sont encore pertinentes de façon à ce que l'ordre n'ait plus d'importance. usable_columns devient un vecteur d'indices de colonnes à traiter duquel je supprime les indices à chaque fois que je rencontre un zéro.

int matrix_elements_sum_indices(const std::vector<std::vector<int>>& matrix)
{
  const int row_size(matrix[0].size());
  std::vector<int> usable_columns(row_size);

  const auto usable_columns_begin(usable_columns.begin());
  auto usable_columns_end(usable_columns.end());

  std::iota(usable_columns_begin, usable_columns_end, 0);

  int result(0);

  for (const std::vector<int>& row : matrix)
    for (auto it(usable_columns_begin); it != usable_columns_end;)
      {
        const int i(*it);
        const int v(row[i]);

        if (v == 0)
          {
            --usable_columns_end;
            *it = *usable_columns_end;
          }
        else
          {
            result += v;
            ++it;
          }
      }

  return result;
}

Alors qu'est-ce que ça donne…

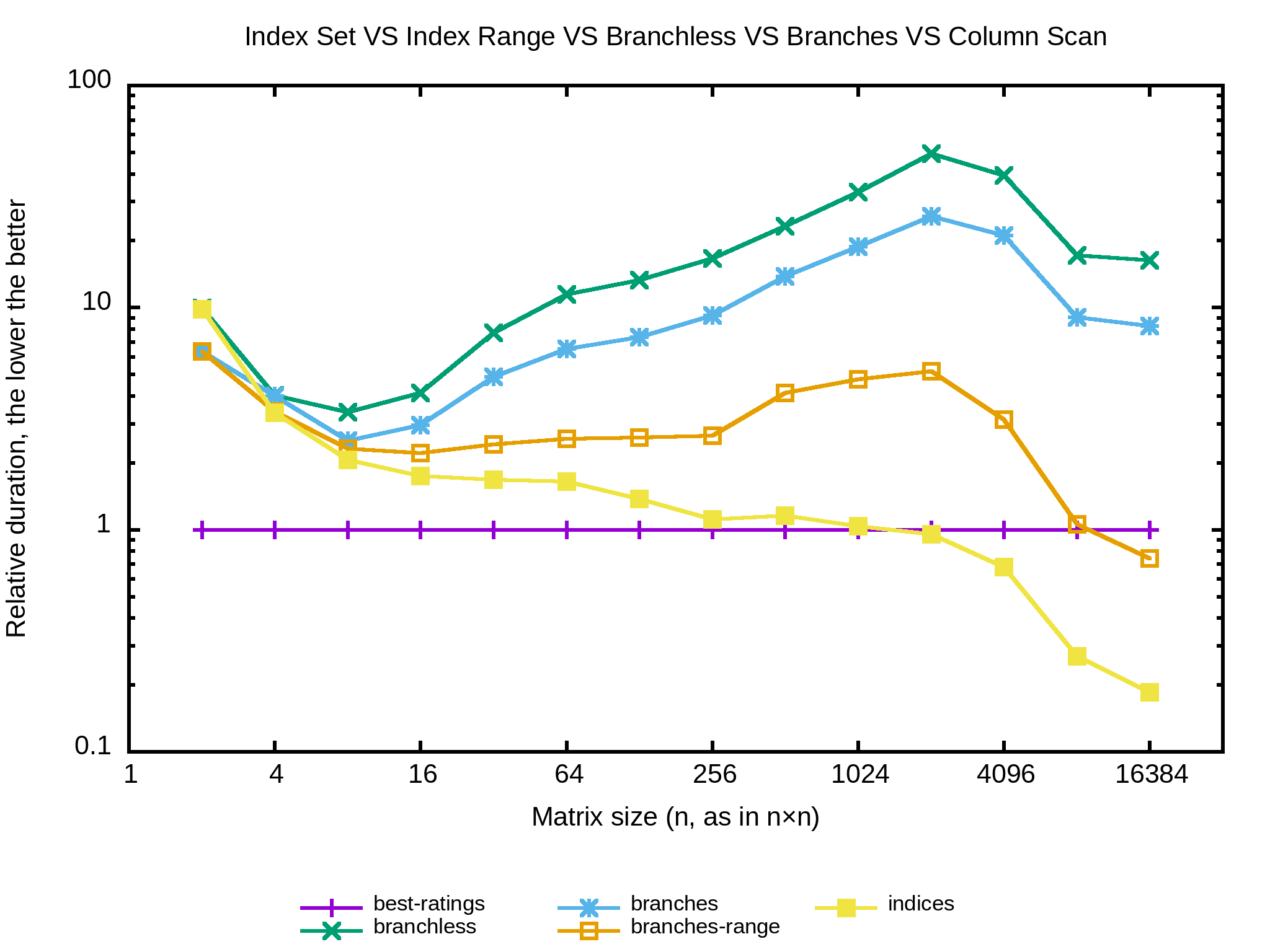
Wouhou ! Ça devient concret, dès 1024×1024 l'algorithme ci-dessus devient plus rapide que l'algo naïf. Quoi d'autre pour l'améliorer ?

La période sombre

Je n'aime pas trop la méthode utilisée pour retirer les indices de usable_columns : l'indice à supprimer est échangé avec le dernier de la liste puis on décrémente le pointeur de fin pour l'ignorer. Je m'attends à ce qu'après quelques itérations les indices soient complètement désordonnés et donc les accès mémoire complètement aléatoires. Est-ce que les performances seraient meilleures en passant un peu de temps à maintenir la liste triée ? Un seul moyen de le savoir :

int matrix_elements_sum_indices_sort
(const std::vector<std::vector<int>>& matrix)
{
  const int row_size(matrix[0].size());
  std::vector<int> usable_columns(row_size);

  const auto usable_columns_begin(usable_columns.begin());
  auto usable_columns_end(usable_columns.end());

  std::iota(usable_columns_begin, usable_columns_end, 0);

  int result(0);

  for (const std::vector<int>& row : matrix)
    {
      for (auto it(usable_columns_begin); it != usable_columns_end;)
        {
          const int i(*it);
          const int v(row[i]);

          if (v == 0)
            {
              --usable_columns_end;
              *it = *usable_columns_end;
            }
          else
            {
              result += v;
              ++it;
            }
        }

      // Cette ligne en plus.
      std::sort(usable_columns_begin, usable_columns_end);
    }

  return result;
}

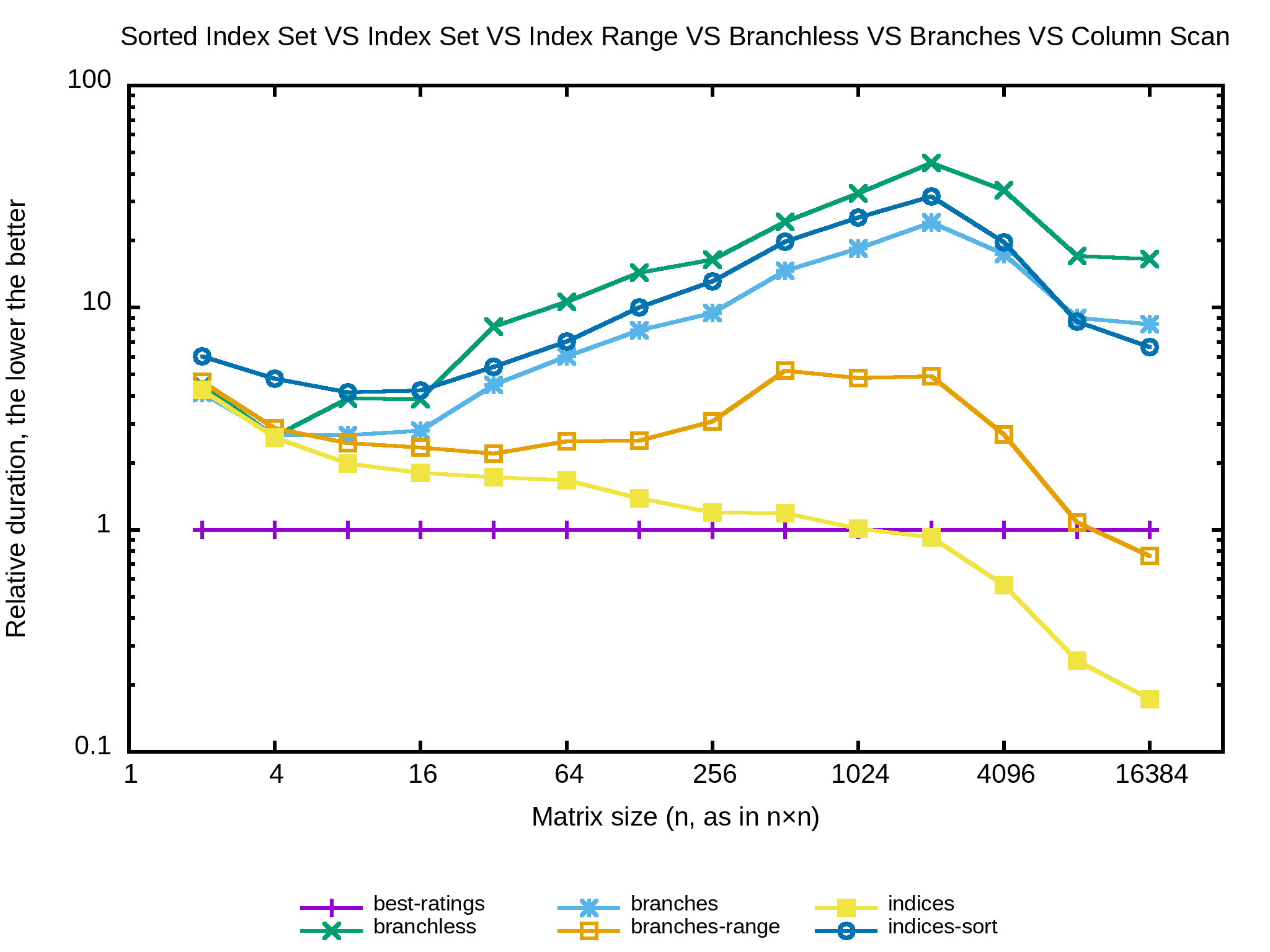
Non. Réponse égale non. Retrier les indices à chaque itération ne compense pas l'hypothétique perte de performances d'accès aléatoires en mémoire. Tentons la suppression de l'indice avec std::vector<>::erase(iterator) et puis une autre implémentation en stockant les indices dans un std::set et encore une autre dans std::unordered_set. Je n'y crois pas trop mais ça me semble important pour la complétude.

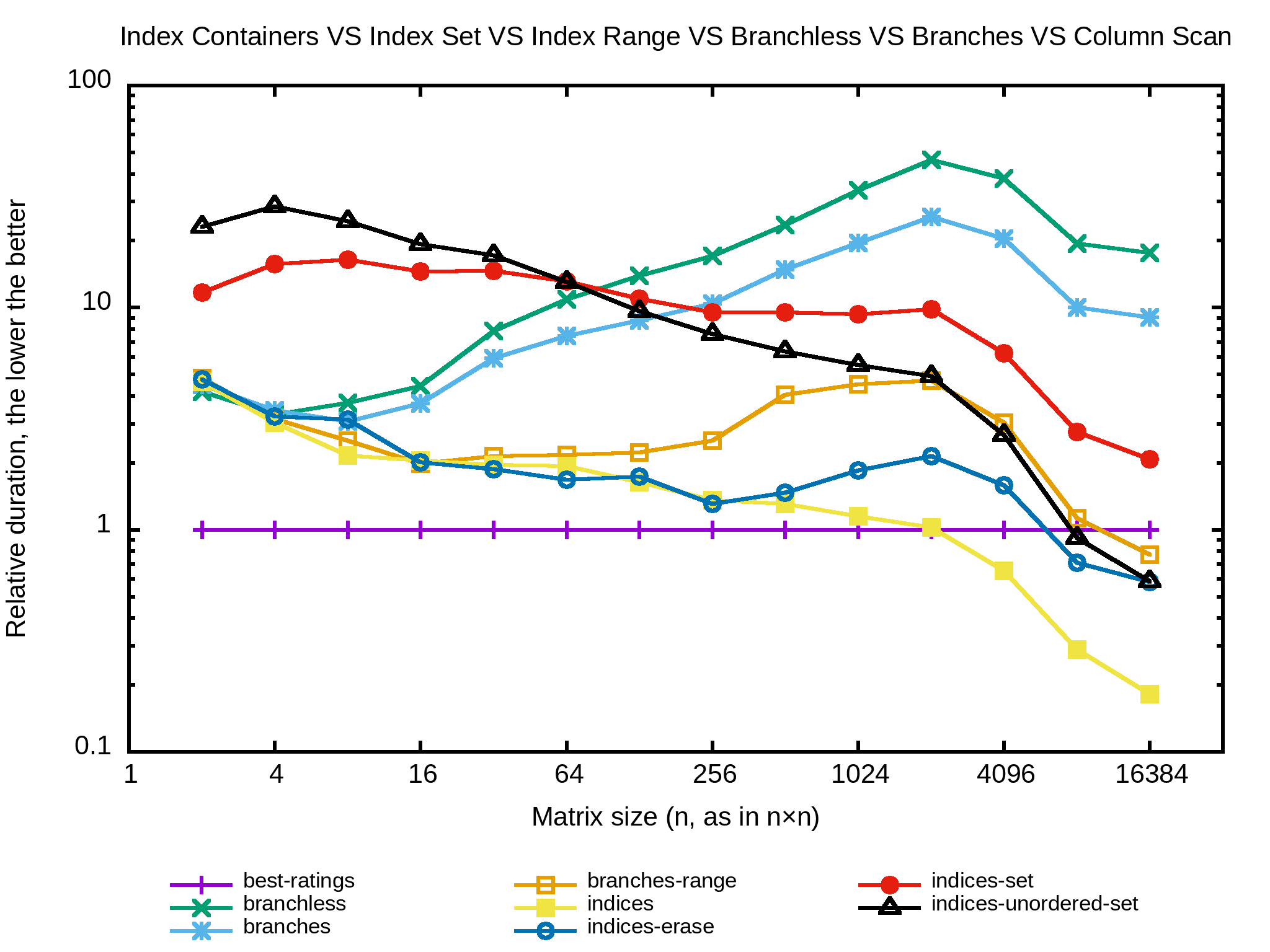
Sans surprise, il n'y a aucun gain ici. Le second meilleur, après l'algo naïf, reste celui qui conserve la liste d'indices dans un std::vector et qui échange les indices supprimés avec le dernier de la collection.

Et si l'algo retournait le résultat dès lors qu'il n'y a plus d'indices à traiter, c’est-à-dire la pratique du return early ? Tiens je vais essayer sur plusieurs des implémentations précédentes pour voir.

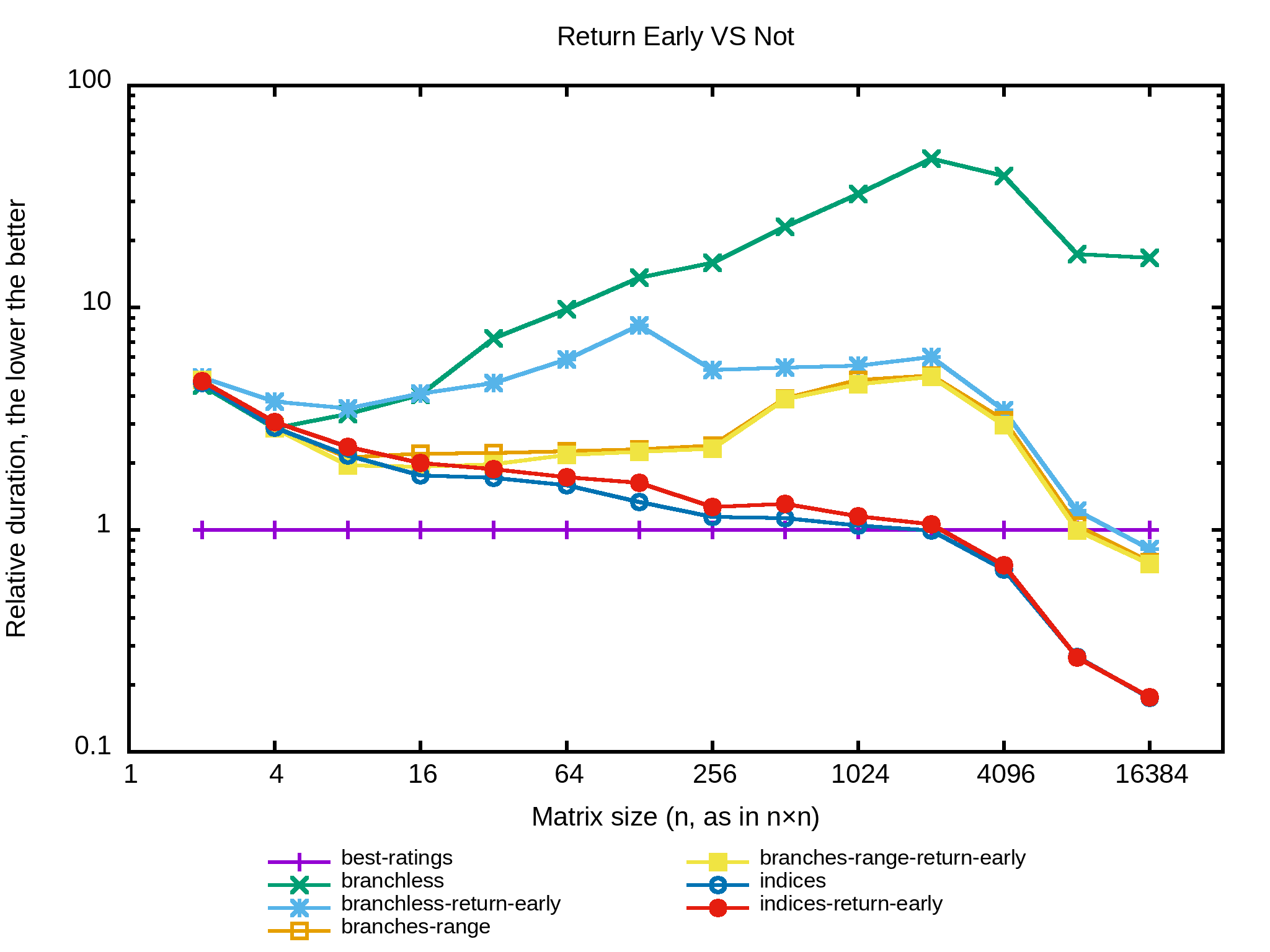
Bon, mauvaises piste. Ça fait partie du jeu de l'optimisation : dès fois on trouve et des fois on se perd. À part pour l'implémentation branchless il n'y a pas d'intérêt à quitter tôt. Cela dit c'est surprenant de voir que la version « indices » se comporte moins bien avec le return early. Est-ce le résultat de mauvaises prédictions du processeur ? Je ne saurais dire.

Continuons sur la version « indices ». La fonction commence par remplir un vecteur avec tous les indices de 1 à n par un appel de std::iota. Est-ce qu'on ne pourrait pas faire mieux en générant un tableau d'indices jusqu'à la taille maximum des matrices dès le début du programme puis initialiser la variable usable_columns à partir de ce tableau ? Nope, ça ne change rien. Crois-moi, j'ai testé.

Tiens, une autre approche classique de l'optimisation, je vais dérouler en partie la boucle la plus interne. L'implémentation commence à être un peu longue alors je vous invite à regarder le code sur GitHub. Il y a plusieurs implémentations :

  • indices_4_by_4 parcours usable_columns par segments de 4 colonnes à la fois et swappe ces indices en branchless de manière à mettre ceux qui ont abouti à zéro à la fin de ce segment, puis les remplace par les valeurs à la fin d'usable_columns.

  • indices_4_by_4_partition fait la même chose mais utilise std::partition pour réordonner le segment.

  • et indices_8_by_8_partition fait de même sur un segment de 8 colonnes.

Et le benchmark :

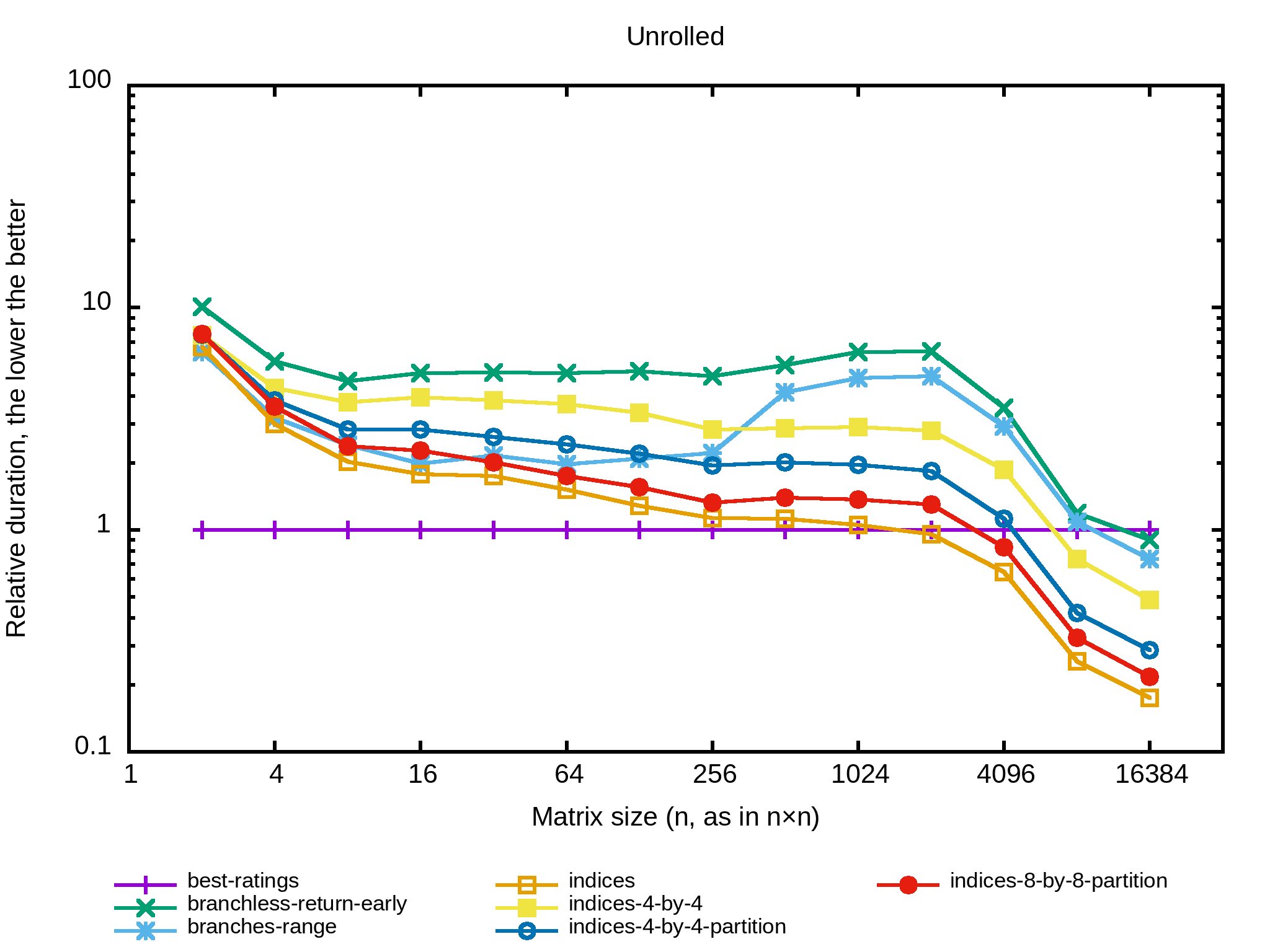
Bon, aucun succès à nouveau. Le compilateur se débrouille clairement mieux que moi pour optimiser la boucle, ce qui n'est pas vraiment surprenant.

Changement d'outils

Un peu à court d'idée je me demande ce que ça donnerait si la matrice était représentée en column-major plutôt que row-major. En d'autres termes, je me demande quel est l'impact de la structure de données sur les performances. Au niveau de l'algorithme ça serait assez direct:

int matrix_elements_sum_column_major(const std::vector<std::vector<int>>& m)
{
  int r(0);

  for (const std::vector<int>& column : m)
    for (int v : column)
      {
        if (v == 0)
          break;

        r += v;
      }

  return r;
}

Et au niveau des performances :

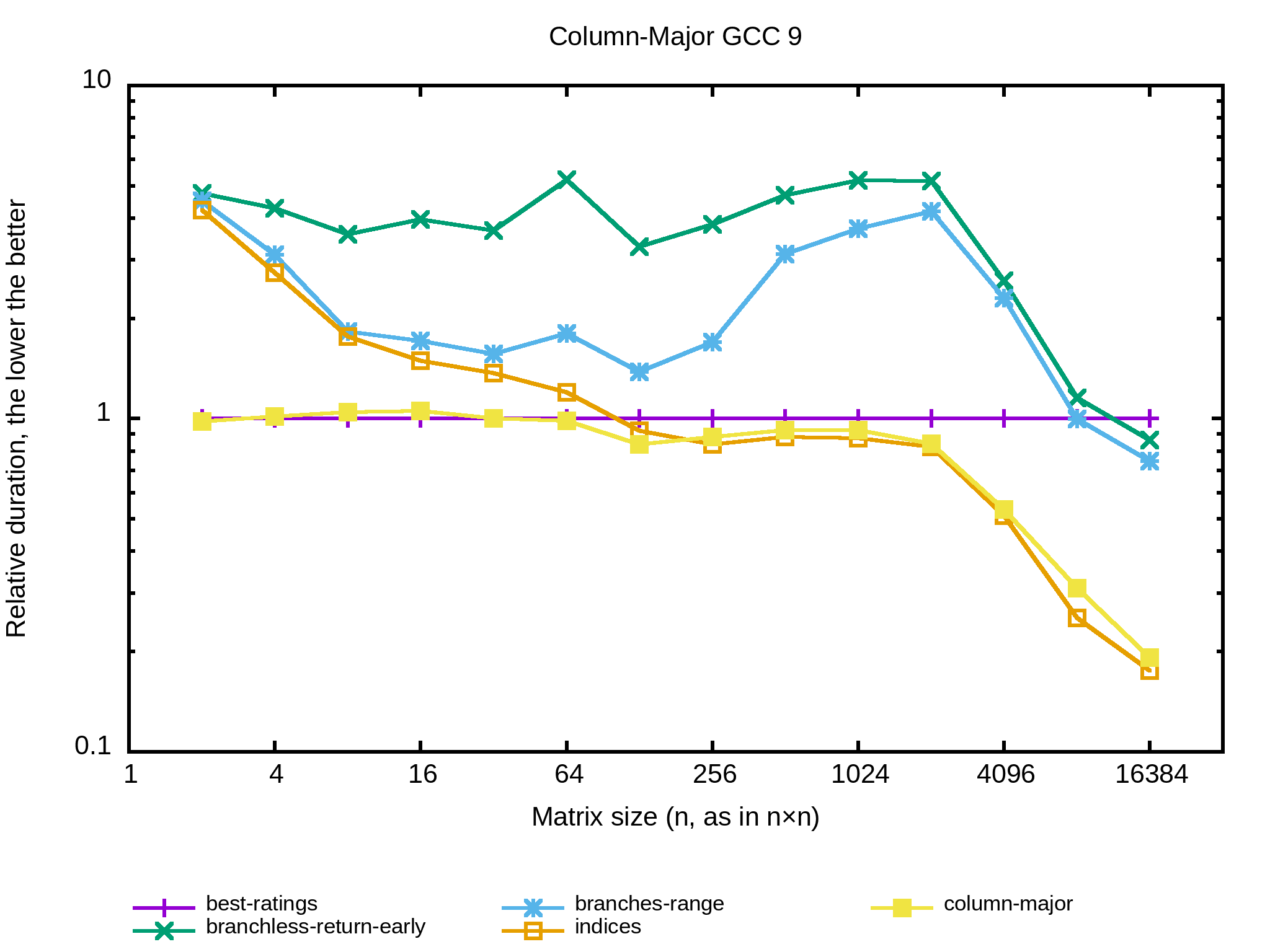
Intéressant, avec une structure de données en column-major les performances sont les mêmes que la meilleure combinaison des algos en row-major vus jusque-là, et l'implémentation est simplissime.

Est-ce qu'un changement de compilateur change aussi les performances relatives des implémentations précédentes ? Essayons avec Clang 9 :

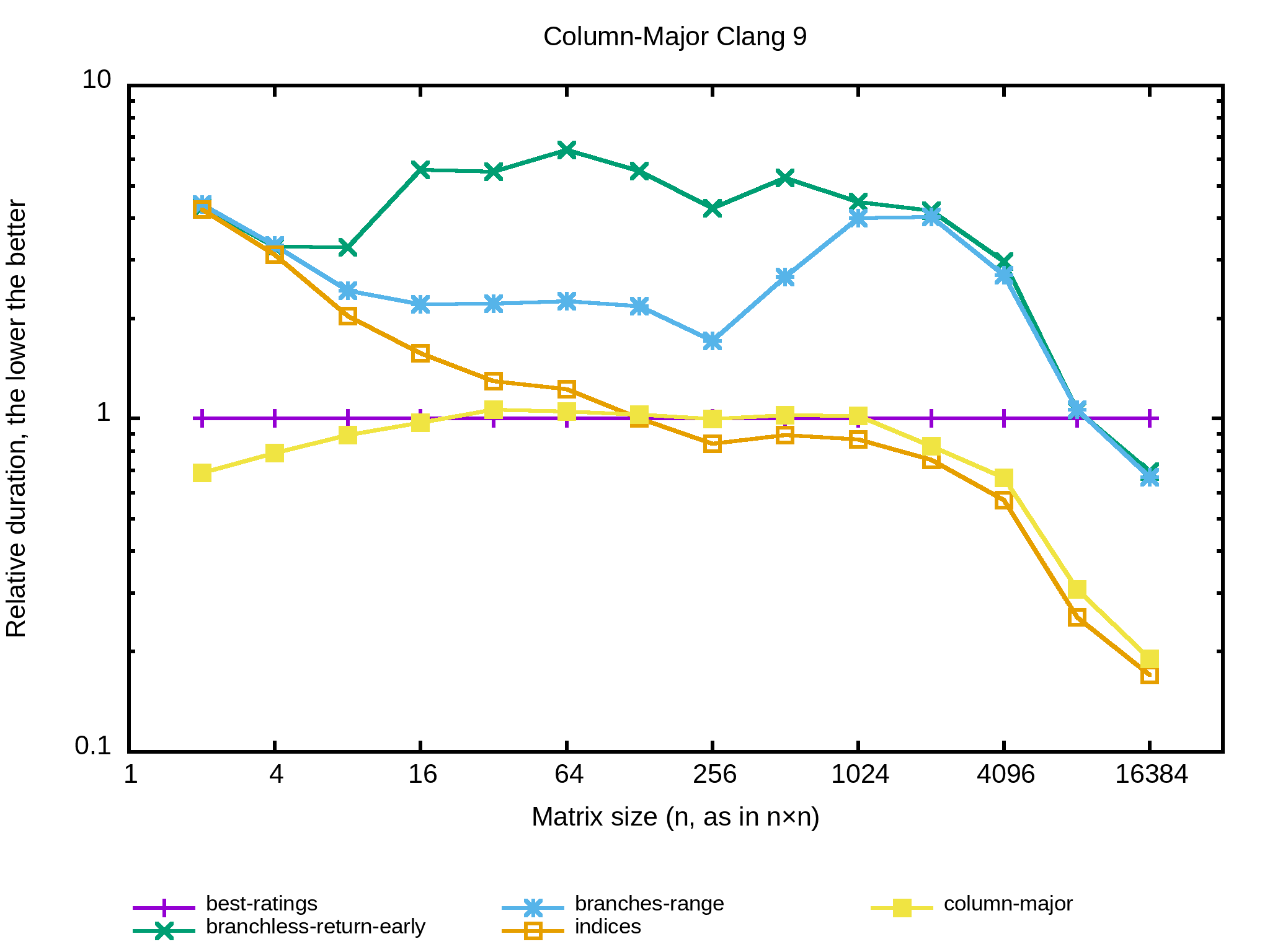
Ça ressemble pas mal aux résultats obtenus avec GCC 9, avec un clair gain pour la structure de données column-major pour les petites tailles. Par contre, cette structure de données perd face à indices en row-major des 256×256. C'est surprenant.

Allez pour finir comparons les performances relatives de Clang et GCC dans un seul graphe. Le programme est compilé avec les deux compilateurs puis lancé sur la seed 1234. Je ne prends que les meilleurs algorithmes vus précédemment :

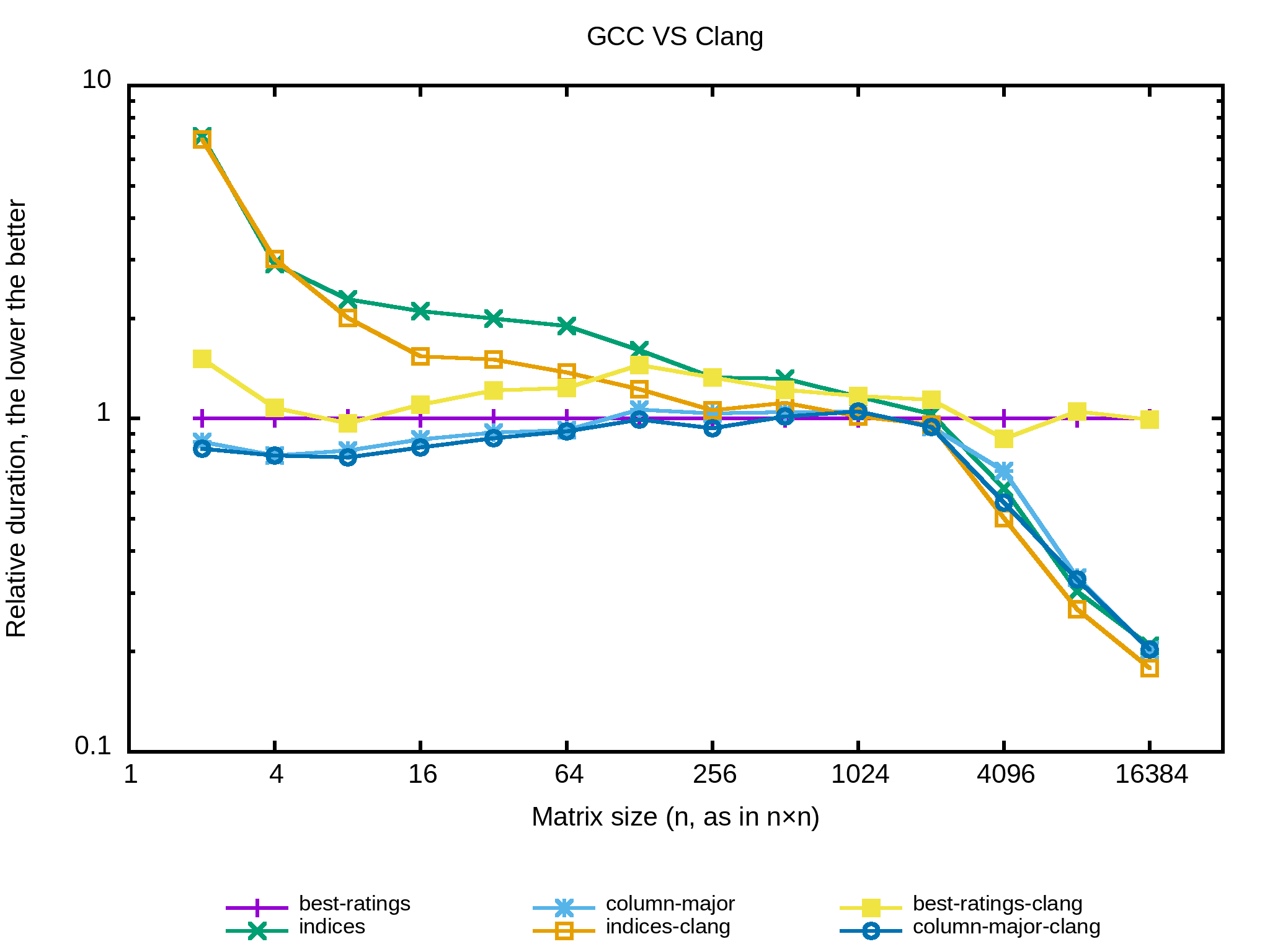
Globalement c'est assez semblable même si Clang se débrouille légèrement mieux sur la version indices et GCC l'emporte à peu de choses sur l'algorithme naïf. Sur la version column-major aucun deux compilateurs ne se démarque.

Il y a quatre ans j'avais effectué des benchmarks qui montraient une forte différence d'optimisations entre GCC et Clang . C'est agréable de voir que les performances des deux compilateurs sont maintenant plutôt proches.

Quand et quoi optimiser

Premature optimization is the root of all evil.

Il est coutume dans le monde des programmeurs d'accueillir par cette citation (amputée) toute tentative d'optimisation d'un code sans avoir d'abord montré son impact sur les performances. La version longue, moins souvent citée, ressemble à ça :

We should forget about small efficiencies, say about 97% of the time: premature optimization is the root of all evil. Yet we should not pass up our opportunities in that critical 3%.
— Donald Knuth

Faut-il pour autant écrire les algorithmes les plus naïfs dès le départ comme pour prévenir toute sorte d'optimisation prématurée ? Eh bien ça dépend. L'algorithme naïf pour le problème considéré ici est performant tant que la matrice est très petite, puis s'écroule rapidement au fur et à mesure que les matrices traitées sont plus grandes. La question qu'il faut alors se poser est « Quel est l'ordre de grandeur des données que mon algo va réellement traiter ? » Autrement dit, est-ce qu'il y a absolument toutes sortes de tailles (ce n'est certainement pas le cas), est-ce que les matrices tiennent toujours dans le cache du processeur ?

Nous avons vu aussi que la structure de données elle-même a un fort impact sur les performances. En passant en column-major un algorithme natif se comporte aussi bien que les meilleurs cas de tous les autres de la version row-major. Ce qui amène à une autre question qui ouvre la porte à d'autres formes d'optimisations : ai-je la main sur la structure de données ? Comment puis-je la transformer pour simplifier mon implémentation et le travail du compilateur ?

En tant que développeur je pense qu'il est bon d'acquérir une certaine culture sur ce que peut faire le matériel qui fait tourner nos programmes ainsi que sur le coût relatif des traitements de nos algorithmes. Non pas pour optimiser tous les cas d'utilisations mais au moins pour ne pas surcharger de traitements inutiles des programmes déjà gourmands. Une sorte de preuve de bonne intention en quelque sorte.

Cette culture s'acquiert par la pratique ; c'est ce que nous apportent ces exercices de programmation. Notamment ici l'approche que je croyais solide (row-major -> scan par ligne) était complètement à la rue sur les petites tailles. On voit alors l'intérêt de pouvoir faire tenir les données dans le cache du processeur. De plus les versions branchless étaient moins performantes que les équivalents branchful (peut-être est-ce juste un manque de savoir faire pour le coup). Ce fut aussi l'occasion de tester un paquet d'implémentations et de constater, à nouveau, l'incroyable travail d'optimisation que font les compilateurs avec notre code.

Finalement ce petit exercice de programmation a amené beaucoup de questions et des réponses parfois surprenantes. J'ai appris des choses donc je pense que ça valait le coup. Nous verrons si les exercices suivants sont aussi enrichissants !

  • # Impact de la structure

    Posté par  . Évalué à 6.

    Merci pour cette (longue) lecture avec une analyse complète et intéressante.

    Je reste curieux de la raison du choix du type la structure pour la matrice, un std::vector<std::vector<int>> plutôt qu'un std::vector<int> de dimension lignes*colonnes, peut-être était-ce un choix délibéré pour la simplicité d'accès aux lignes/colonnes. Ça reste acceptable vu la contraire initiale de la taille de matrice d'ordre 10×10. Cela dis, si on cherche les meilleures performance possible, ce point n'est probablement pas négligeable et ce std::vector<std::vector<int>> me jette quelques grains de sable dans les yeux, pour plusieurs raisons :
    * std::vector est un conteneur qui stocke les données de façon contiguë dans une zone mémoire allouée dynamiquement. Grossièrement, la structure est composée de trois pointeurs : début/fin de la zone allouée, et première "case" libre (ça peut varier selon l'implémentation)
    * std::vector<std::vector<int>> est donc une structure qui pointe sur une zone allouée dynamiquement, qui elle contient des std::vector<int> qui chacun d'entre eux pointent sur d'autres zones allouées dynamiquement
    * Il y a déjà un impact à l'initialisation, puisqu'il faudra allouer autant de zones que les dimensions de la matrice le nécessite (mais c'est hors benchmark ici)
    * Il n'y a aucune garantie que toutes ces "petites zones" soie allouée de façon contiguë (c'est plutôt improbable), donc on augmente le risque de cache-miss
    * Je ne m'étends pas sur le surcoût d'utilisation de mémoire induit par la structure

    Je serais curieux de comparer ces résultats à ceux exploitant une représentation de la matrice dans une seule zone continue (par ex avec un std::vector<int>). J'aurais bien voulu ajouter un comparatif à ce commentaire, mais je ne vais malheureusement pas avoir le loisir de m'amuser avec ce problème dans les prochain temps.

    • [^] # Re: Impact de la structure

      Posté par  (site web personnel) . Évalué à 5. Dernière modification le 12 février 2020 à 08:02.

      C'est un cas intéressant maths vs informatique : des structures [ligne][colonne], [colonne][ligne] ou [ligne x colonne] sont mathématiquement équivalentes et informatiquement très différentes (en termes de performances mémoire ou disque, pas fonctionnellement).

      • [^] # Re: Impact de la structure

        Posté par  . Évalué à 3.

        Mais std::vector<std::vector<int>> n'est pas du tout équivalent à une matrice, car la longueur de chaque "ligne" peut changer. Tu peux probablement montrer que pour toute structure de donnnées qui permet une longueur de "ligne" variable, il existe une structure à longueur de "ligne" fixe plus efficace.

        Du coup je ne vois pas ça comme une différence entre maths et info, mais plutôt comme une structure de donnée trop flexible par rapport à la représentation mathématique cherchée.

  • # Quitte à faire du branchless

    Posté par  (site web personnel) . Évalué à 4.

    Je te propose cette légère amélioration :

    int matrix_elements_sum_branchless_2(const std::vector<std::vector<int>>& matrix)
{
  const int row_size(matrix[0].size());
  std::vector<int> usable_column(row_size, -1);

  int result(0);

  for (const std::vector<int>& row : matrix)
    for (int i(0); i != row_size; ++i)
      {
        const int v(row[i]);
        result += v & usable_column[i];
        usable_column[i] &= v ? -1 : 0;
      }

  return result;
}

    Elle a l'avantage de se vectoriser très bien, et d'éviter le passage par une multiplication. Elle reste moins bonne que la version de référence, sauf dans les cas dégénérés (pas de zéro p.e.). On notera qu'on pourrait aussi passer la boucle interne sous OpenMP :-)

    Cas dégénéré : http://quick-bench.com/PTIzGKHuheFGyKEVjkAPBwgDo4s
    Cas normal : http://quick-bench.com/goZHQlQ10U4sDqMiEP0nMyyXUBs

    Merci pour ce petit jeu d'esprit !

    • [^] # Re: Quitte à faire du branchless

      Posté par  (site web personnel) . Évalué à 2.

      Bien vu pour la version sans multiplication :) On voit bien la vectorisation et ça marche bien mieux :

      2020-02-12 08:34:50
Running ./build/matrix-elements-sum-GNU
Run on (4 X 3100 MHz CPU s)
CPU Caches:
  L1 Data 32 KiB (x2)
  L1 Instruction 32 KiB (x2)
  L2 Unified 256 KiB (x2)
  L3 Unified 3072 KiB (x1)
Load Average: 0.67, 0.67, 0.63
***WARNING*** CPU scaling is enabled, the benchmark real time measurements may be noisy and will incur extra overhead.
-------------------------------------------------------------
Benchmark                   Time             CPU   Iterations
-------------------------------------------------------------
branchless/2             28.4 ns         28.4 ns     24540986
branchless/4             45.6 ns         45.6 ns     15164641
branchless/8              116 ns          116 ns      5777179
branchless/16             369 ns          369 ns      1898641
branchless/32            1387 ns         1387 ns       484254
branchless/64            5847 ns         5846 ns       111630
branchless/128          22439 ns        22436 ns        30474
branchless/256          88132 ns        88125 ns         7754
branchless/512         349637 ns       349573 ns         2010
branchless/1024       1441557 ns      1441252 ns          485
branchless/2048       5766216 ns      5764464 ns          121
branchless/4096      22847843 ns     22846967 ns           31
branchless/8192      91376681 ns     91368790 ns            8
branchless/16384    367024190 ns    366997034 ns            2
branchless_2/2           34.7 ns         34.7 ns     20037235
branchless_2/4           40.5 ns         40.5 ns     17081915
branchless_2/8           62.9 ns         62.9 ns     10383991
branchless_2/16           146 ns          146 ns      4770697
branchless_2/32           435 ns          435 ns      1600480
branchless_2/64          1869 ns         1863 ns       450005
branchless_2/128         5882 ns         5882 ns       104268
branchless_2/256        24406 ns        24407 ns        28618
branchless_2/512       100493 ns       100124 ns         7202
branchless_2/1024      473645 ns       473618 ns         1248
branchless_2/2048     2284499 ns      2284170 ns          288
branchless_2/4096     6951965 ns      6951809 ns           79
branchless_2/8192    33005646 ns     33002903 ns           20
branchless_2/16384  118768214 ns    118758699 ns            5

    • [^] # Re: Quitte à faire du branchless

      Posté par  . Évalué à 1.

      Je me suis permis d'ajouter à ce bench l'implémentation que je proposais dans mon commentaire, pour mettre en évidence l'impact du choix de la structure de donnée sur les perfs :

      http://quick-bench.com/lSIBctcUoFcxRNSssMJTMy93Zfg

      On constate (pour les paramètres donnés) que l'intuition initiale du rédacteur sur la version branchless se retrouve dans ce cas. L'écart de performances de la version branchless "avec multiplication" par rapport au autres versions se réduit avec une structure contiguë en mémoire.

    • [^] # Re: Quitte à faire du branchless

      Posté par  (site web personnel) . Évalué à 2.

      Tiens, dis-moi, j'essaye le même genre de truc sur la version indices, qui maintient une liste les indices des colonnes pertinentes :

      int matrix_elements_sum_indices_branchless
(const std::vector<std::vector<int>>& matrix)
{
  const int row_size(matrix[0].size());
  std::vector<int> usable_columns(row_size);

  const auto usable_columns_begin(usable_columns.begin());
  auto usable_columns_end(usable_columns.end());

  std::iota(usable_columns_begin, usable_columns_end, 0);

  int remaining_count(row_size);
  int result(0);

  for (const std::vector<int>& row : matrix)
    for (auto it(usable_columns_begin); it != usable_columns_end; )
      {
        const int i(*it);
        const int v(row[i]);
        result += v;

        const int keep_mask((v == 0) ? 0 : -1);
        usable_columns_end += ~keep_mask;

        // discussion ci-dessous sur le code d'ici…
        const int distance_to_last(usable_columns_end - it);
        const auto new_i_it(it + (distance_to_last & ~keep_mask));
        *it = *new_i_it;
        // …à là.

        it += -keep_mask;
      }

  return result;
}

      Ça ne fonctionne pas très bien et je pense que c'est à cause de l'écriture dans le bloc d'ici à là. Si je mets à la place de ce bloc la condition suivante :

              if (~keep_mask)
          *it = *usable_columns_end;

      Alors ça fonctionne très bien.

      Ma compréhension est grosso-modo que dans la première version on réécrit inconditionnellement dans la mémoire pointée par it, et bien qu'elle est probablement en cache (on vient juste d'y accéder) et que sa valeur ne change pas toujours, la ligne de cache devient toujours dirty et il faut la renvoyer en RAM. Du coup on paye une écriture à chaque itération, qui coûte bien plus cher qu'une misprediction occasionnelle. Qu'en penses tu ?

  • # best-rating == column-major

    Posté par  (site web personnel) . Évalué à 2.

    Je n'aurais pas appelé "branchless" un algorithme avec des boucles for. Pour 

        result += v * usable_column[i];
    usable_column[i] *= (v != 0);

    Ce n'est pas évident que ce branchement soit inliné, il aurait été bien d'avoir un extrait du code assembleur, et de comparer avec une version sans multiplication.

    Pour faire vraiment de l'optimisation CPU, il faut presque obligatoirement un "profiler" pour observer l'impact des accès mémoire sur le binaire optimisé. Il faut donc faire un peu d'assembleur, c'est la partie la plus intéressante. Enfin, le C ou même le Fortran simplifie ce travail et offre plus de liberté par rapport au C++ (on peut toujours faire du C dans du C++ ??).

    Le meilleur est celui qui accède à la mémoire de façon contiguë, en en faisant le moins. Comme les matrices sont de tailles fixes, on peut imaginer d'autres optimisations, du style en C, accéder à la prochaine adresse pour chauffer le cache sans rien faire, du prefetch, donner de la visibilité au compilateur en déroulant un peu ces boucles ou en utilisant des indices connus à la compilation.. , mais on navigue en aveugle sans un extrait du code désassemblé.

    • [^] # Re: best-rating == column-major

      Posté par  (site web personnel) . Évalué à 2. Dernière modification le 12 février 2020 à 09:17.

      Ce n'est pas évident que ce branchement soit inliné, il aurait été bien d'avoir un extrait du code assembleur, et de comparer avec une version sans multiplication.

      Bien vu ! Voici une version sur Compiler Explorer où on peu voir le corps de la version branchless :

      .L31:
        mov     rdx, QWORD PTR [r8]
        movsx   ecx, BYTE PTR [rdi+rax]
        mov     edx, DWORD PTR [rdx+rax*4]
        mov     esi, ecx
        imul    ecx, edx
        add     r12d, ecx
        test    edx, edx
        setne   dl
        and     edx, esi
        mov     BYTE PTR [rdi+rax], dl
        mov     rdx, rax ; à partir de là on gère le compteur de la boucle et
        add     rax, 1   ; la condition de sortie.
        cmp     r9, rdx
        jne     .L31     ; on a un seul jump par itération.

      et celui avec les branches :

      .L70:
        mov     BYTE PTR [rdi+rax], 0 ; usable_column[i] = 0
.L53:
        lea     rdx, [rax+1] ; gestion du compteur de la boucle, sans intéret
        cmp     rcx, rax     ; pour la comparaison de la sortie asm
        je      .L52         ; saut pour sortir de la boucle
.L59:
        mov     rax, rdx     ; fin de la gestion du compteur de la boucle
.L55:
        cmp     BYTE PTR [rdi+rax], 0
        je      .L53 ; un premier jump hors gestion du compteur de la boucle
        mov     rdx, QWORD PTR [rsi]
        mov     edx, DWORD PTR [rdx+rax*4]
        test    edx, edx
        je      .L70 ; là on a un jump qui va nous permettre de faire
                     ; l'affectation usable_column[i] = 0 puis d'enchaîner avec
                     ; la gestion du compteur de la boucle.
                     ; Ça fusionne les deux sauts du code initial (le test
                     ; if (v==0) puis le saut pour reboucler.
        add     r12d, edx ; result += v
        lea     rdx, [rax+1] ; à nouveau de la gestion du compteur de boucle
        cmp     rcx, rax
        jne     .L59

  • # Lisibilité

    Posté par  (site web personnel) . Évalué à 10.

    C'est un journal intéressant en recherche de performances pures, mais faut pas oublier un truc qui parfois fait gagner en performances globales : la lisibilité du code.

    Je m'explique : un code super optimisé qui te fait gagner une seconde de traitement sur un script qui s'exécute tous les jours, ça fait gagner 3 minutes en 6 mois. Mais si au bout de ces 6 mois tu mets 3 heures à déchiffrer comment marche ce putain de code que tu veux modifier, tu as globalement perdu 2h57m (et encore, j'estime que mon temps de vie est plus important que le temps processeur perdu, chacun ses priorités).

    Donc oui, c'est un bon exercice mental, c'est même extra de se pencher là dessus de manière aussi détaillée, … tant que ça reste un jeu de l'esprit.
    En entreprise, en prod, on va essayer de trouver un équilibre, un compromis, entre performance et lisibilité, histoire de ne pas perdre des heures plus tard si le code doit être légèrement modifié. On a probablement tous haï des gars qui ont fait des codes trop tarabiscotés dans le but de gagner un pouillème.

    • [^] # Re: Lisibilité

      Posté par  . Évalué à 4.

      Mais si c'est un code qui est exécuté sur des milliers de produits et/ou chez des milliers de clients, le rapport temps gagné/temps dépensé est nettement plus favorable à l'optimisation.

    • [^] # Re: Lisibilité

      Posté par  . Évalué à 5.

      On a probablement tous haï des gars qui ont fait des codes trop tarabiscotés dans le but de gagner un pouillème.

      Jamais. J'ai haï les gens qui n'ont pas couverts leur code par des tests. J'ai aucun problème pour que quelqu'un ai pensé faire quelque chose d'un peu complexe, mais :

      • il faut que ce soit limité : tu cache ça dans une unité de code limité ça ne doit pas fuir dans le reste du code
      • il faut avoir tester ce code : je vois pas comment on peut optimiser du code sans avoir de tests unitaire pour s'assurer que l'optimisation ne pète pas le fonctionnel

      Si tu as ça, il n'y a aucun problème à déployer des trésors de subtilité.

      Après oui la lisibilité est importante1 et il faut voir si optimiser est intéressant. Mais là il s'agit d'un exercice d'optimisation donc on va considérer que c'est utile ;)

      1. par exemple je vais préférer utiliser 0xff_ff_ff_ff ou ~0 plutôt que -1 comme valeur d'entier quand il est utiliser comme bit patterns. ↩

      https://linuxfr.org/users/barmic/journaux/y-en-a-marre-de-ce-gros-troll

      • [^] # Re: Lisibilité

        Posté par  (site web personnel) . Évalué à 3.

        Jamais. J'ai haï les gens qui n'ont pas couverts leur code par des tests. J'ai aucun problème pour que quelqu'un ai pensé faire quelque chose d'un peu complexe,

        Voilà pourquoi j'ai mis un "probablement" dans ma phrase, je me doutais qu'il existe des exceptions, chanceux va !

        Je me souviens d'avoir du modifier des codes écrits en GAP3 (sur AS/400) écrits par un gars que je n'ai pas connu personnellement, mais que j'ai traité de tous les noms. Et puis j'ai un peu regretté quand j'ai appris que le gars s'était suicidé (avant que j'arrive, po ma faute, hein). La psychologie d'une personne influence-t-elle sa façon de coder ? Moi, j'y crois. Faire des usines à gaz pour gagner des queues de cerises, en comptant le temps qu'il a du y passer et le mien à m'arracher les cheveux, le jeu n'en valait pas la chandelle.

        Après, il existe bien entendu des cas spéciaux où l'optimisation pure est LA priorité, mais c'est marginal.
        Le sujet du journal, oui, c'est utile car l'optimisation pure est le but du jeu, jeu qui justement peut être utile dans ces cas spéciaux.

        • [^] # Re: Lisibilité

          Posté par  . Évalué à 1. Dernière modification le 12 février 2020 à 11:50.

          Voilà pourquoi j'ai mis un "probablement" dans ma phrase, je me doutais qu'il existe des exceptions, chanceux va !

          Je pense que tu a raté ma remarque. J'ai râlé sur les même personnes, mais je considère que le problème n'est pas tant leur code que le fait qu'ils n'ont pas écrit de test.

          Après, il existe bien entendu des cas spéciaux où l'optimisation pure est LA priorité, mais c'est marginal.

          Non, c'est une question de domaine. L'optimisation CPU de code n'est pas majoritaire, mais on peut difficilement dire que c'est marginal, mais la gestion de la performance (ce qui peut être très différent) n'est pas marginale du tout.

          https://linuxfr.org/users/barmic/journaux/y-en-a-marre-de-ce-gros-troll

        • [^] # Re: Lisibilité

          Posté par  (site web personnel) . Évalué à 2.

          Et puis j'ai un peu regretté quand j'ai appris que le gars s'était suicidé (avant que j'arrive, po ma faute, hein). La psychologie d'une personne influence-t-elle sa façon de coder ?

          Ou bien l'inverse : la façon de coder influence sa psychologie.
          Péter un câble car on n'arrive même plus à comprendre son propre code tout pourri.

          --> []

    • [^] # Lisibilité… et optimisation là où c'est utile !

      Posté par  (site web personnel, Mastodon) . Évalué à 9. Dernière modification le 12 février 2020 à 11:43.

      Personnellement je n'ai pas de problème à voir du code peu lisible pour des questions d'optimisation, à partir du moment où :

      1. C'est documenté – l'auteur a expliqué pourquoi et comment le code tarabiscoté a été conçu,
      2. C'est testé – parce que si le code est difficile à lire, c'est aussi difficile de savoir ce qu'il fait,
      3. C'est isolé – c'est un morceau de code tordu, pas l'intégralité du code qui est tordue.
      4. C'est utile.

      C'est bizarre, mais le point 4 est en fait assez rare. Je ne compte plus les trouzaines de micro-optimisations complètement inutiles alors que juste à côté il y a un énorme problème de performances facile à corriger.

      J'ai l'impression que beaucoup de (mauvais ?) développeurs optimisent sur ce qu'ils pensent être problématique, au lieu de mesurer ce qui est réellement problématique. Et c'est comme ça qu'on se retrouve avec des trucs tordus pour gagner 0.5 ms sur une page qui met 15 secondes pour être calculée. Ou une astuce pour gagner quelques Ko de RAM, alors qu'une structure censée stocker des dizaines de millions d'entrée en RAM est tellement pétée qu'il lui faut 280 octets pour stocker un double (8 octets) (et donc, 10 millions d'entrées prennent 2,8 Go de RAM pour 80 Mo de données utiles) (je précise que la structure n'offre aucun avantage sur un tableau)…

      On a certes dépassé la grande époque de PHP et des conseils moisis à base de « Utilise des guillemets simples, c'est plus rapide que les guillemets doubles », mais c'est encore des problèmes que je rencontre souvent.

      La connaissance libre : https://zestedesavoir.com

  • # projet euler

    Posté par  (site web personnel) . Évalué à 6.

    moi j'ai testé mes limites en programmation et les limites de ma machine avec https://projecteuler.net/

    La méthode bourrin ne marche jamais. Donc il faut trouver un algo approprié.

    Donc c'est plus un exercice de math avec une recherche d'algo. Mais ca rejoint les besoins d'optimisation.

    Je suis que niveau 2 /o\ sur le site ….

    • [^] # Re: projet euler

      Posté par  . Évalué à 3.

      La méthode bourrin ne marche jamais sur les exo du project Euler, dans la vraie vie, faut voir..

  • # du pourquoi du comment

    Posté par  . Évalué à 4.

    Cela signifie que sur des entiers de 32 bits les matrices en dessous de 64×64 tiennent dans un
    cache L1, puis dans L2 jusqu'à 128×128, puis L3 jusqu'à 512×512.
    Au delà il faudra aller chercher les données en RAM.

    En fait, la situation est pire encore: au delà, on se paye des défaut de cache et on perd des centaines de cycles.

    Reste à voir si les performances sont meilleures parce qu’on a supprimé les branches, ou parce que l'on a réussi à se coller pile poil à la taille des caches…

    Après, ça devient compliqué puisque l'on optimise en fonction du hardware qui tourne en dessous.

    • [^] # Re: du pourquoi du comment

      Posté par  (site web personnel) . Évalué à 5.

      C'est vraiment la question que je me pose à chaque fois quand je lis ce genre d'optimisation. Combien sont spécifiques à la machine hôte, et combien vont encore fonctionner sur une machine avec une config hardware légèrement ou fondamentalement différente ?

  • # Et la version courte ?

    Posté par  (site web personnel) . Évalué à 2.

    J'avoue que sur ces exercices de programmation, j'adore la partie qui consiste à chercher le programme le plus court qui résout le problème. Surtout en Python, en jouant sur le langage, on arrive à gratter pas mal par rapport à la solution de base.

    Par contre, s'il y a un codeur ruby dans le challenge, aucune chance. Ce langage est vraiment très concis!

    • [^] # Re: Et la version courte ?

      Posté par  (site web personnel) . Évalué à 6.

      Une version possible en Ruby :

      def sum(matrix)
  matrix.transpose.map do |column|
    column.take_while { |n| n != 0 }.sum
  end.sum
end

m = [
  [0, 2, 3],
  [1, 0, 4],
  [5, 6, 7],
]

puts sum(m) # => 16

      • [^] # Re: Et la version courte ?

        Posté par  . Évalué à 3.

        La même chose en Haskell :

        import Data.List

msum =
  sum . map sum . map (takeWhile $ (<) 0) . transpose

main = do
  print $ msum [[0, 2, 3],[1, 0, 4],[5, 6, 7]]

  • # C++ boost

    Posté par  (site web personnel) . Évalué à 4.

    Peut être qu'avec un soupçon de boost, tu aurais des perfs équivalentes et un code plus élégant?

        #include <boost/numeric/ublas/matrix.hpp>
    #include <boost/numeric/ublas/assignment.hpp>
    #include <boost/numeric/ublas/io.hpp>

    int main () {
        using namespace boost::numeric::ublas;
        matrix<int> m (3, 3);
        m <<= 0, 2, 3,
              1, 0, 4,
              5, 6, 7;

        int sum = 0;
        for (unsigned i = 0; i < m.size1 (); ++i) {
           sum += m(0, i);
        }
        for (unsigned j = 1; j < m.size2 (); ++j) {
            for (unsigned i = 0; i < m.size1 (); ++i) {
               if( m (j-1, i) ) {
                   sum += m(j, i);
               } else {
                   m(j, i) = 0;
               }
            }
        }
        std::cout << sum << std::endl;
    }

    Le post ci-dessus est une grosse connerie, ne le lisez pas sérieusement.

  • # benchmarks latence et bande passante CPU en 2020

    Posté par  (Mastodon) . Évalué à 2.

    Un autre benchmark qui fait suite à un article de 2012 souvent donné comme référence (Numbers Every Programmer Should Know) permet de voir comment la latence et la bande passante des processeurs a progressé en 8 ans.

    https://www.forrestthewoods.com/blog/memory-bandwidth-napkin-math/

    l'auteur note que l'article original donnait des chiffres qui était (au moins pour le premier d'entre eux) un peu sujets à caution :

    L1 cache reference                           0.5 ns
Branch mispredict                            5   ns
L2 cache reference                           7   ns                      14x L1 cache
Mutex lock/unlock                           25   ns
Main memory reference                      100   ns                      20x L2 cache, 200x L1 cache
Compress 1K bytes with Zippy             3,000   ns        3 us
Send 1K bytes over 1 Gbps network       10,000   ns       10 us
Read 4K randomly from SSD*             150,000   ns      150 us          ~1GB/sec SSD
Read 1 MB sequentially from memory     250,000   ns      250 us
Round trip within same datacenter      500,000   ns      500 us
Read 1 MB sequentially from SSD*     1,000,000   ns    1,000 us    1 ms  ~1GB/sec SSD, 4X memory
Disk seek                           10,000,000   ns   10,000 us   10 ms  20x datacenter roundtrip
Read 1 MB sequentially from disk    20,000,000   ns   20,000 us   20 ms  80x memory, 20X SSD
Send packet CA->Netherlands->CA    150,000,000   ns  150,000 us  150 ms

    Et que maintenant, sur un i7 il a pu en gros calculer la latence suivante

    L1 CACHE hit, ~4 cycles(2.1 - 1.2 ns)
L2 CACHE hit, ~10 cycles(5.3 - 3.0 ns)
L3 CACHE hit, line unshared               ~40 cycles(21.4 - 12.0 ns)
L3 CACHE hit, shared line in another core ~65 cycles(34.8 - 19.5 ns)
L3 CACHE hit, modified in another core    ~75 cycles(40.2 - 22.5 ns)
local  RAM                                                   ~60 ns

    et pour la bande passante :

    Memory Bandwidth: 39.74 gigabytes per second
L1 cache: 192 kilobytes (32 KB per core)
L2 cache: 1.5 megabytes (256 KB per core)
L3 cache: 12 megabytes  (shared; 2 MB per core)

  • # Euuuhhhh....

    Posté par  . Évalué à -2.

    C'est pas que je veux troller comme un sagouin, mais j'ai l'impression que tout ce journal et une bonne partie des commentaires n'est qu'une gigantesque branlette intellectuelle qui ne va nulle part. Je suis un peu désolé de dire ça de but en blanc, pour une fois qu'on a un journal qui met les mains dans le cambouis.

    Je reprends la solution best rating et je remplace les entêtes des boucles for par ceux (+ ou -) de indices, et là, boum, j'ai un x10 sur des grosses matrices qui renvoie tous les concurrents chez leur mère respective :

        for (const std::vector<int>& row : m) {
        for (const int &e : row) {
            if (e == 0)
                break;
            r += e;
        }
    }

    Je précise que je suis une grosse tanche en C++ (juste qq vagues connaissances en copier/coller), langage qui n'est lui même qu'une gigantesque branlette dont la syntaxe est en train d'évoluer vers un délire cabalisto-confusionniste et dont le but, comme ce journal le démontre, n'est que se répandre en débats intranchables car personne de normalement constitué n'est capable de comprendre ce que peut bien faire le compilo de tout ce gloubi-boulga indigeste (à part nous balancer des messages d'erreur encore moins compréhensible qu'un stack dump).

    • [^] # Re: Euuuhhhh....

      Posté par  (site web personnel) . Évalué à 10.

      Ta solution est sans doute très efficace, malheureusement elle ne répond pas à la question ! Le but est d'ignorer les valeurs pour lesquelles il existe un zéro plus haut dans la même colonne. Là ton algo ignore le reste de la ligne quand il rencontre un zéro.

      Ça fonctionnerait si la matrice était en column-major, ce qui est d'ailleurs pris en considération dans le journal, mais ça demande de changer la structure de donnée. C'est un peu tricher par rapport à l'exercice. J'aurais bien voulu croire que tu considères que la matrice est en column-major mais comme tu as nommé ta variable row je ne doute pas que tu la considères en row-major.

      En tout cas merci pour les insultes et le mépris, c'est top ! <3

      • [^] # Re: Euuuhhhh....

        Posté par  . Évalué à 7.

        Il n'y avait pas d'insulte contre toi, juste contre le C++… après c'est vrai le mépris a un peu débordé sur le journal, et je reconnais après coup que c'était totalement déplacé : effectivement, le remplacement que j'ai opéré change complètement l'algo, et je me suis auto-abusé en imaginant c'était le compilo qui optimisait simplement une syntaxe mieux qu'une autre, perdu que j'étais à essayer de comprendre ce n-ième style de C++.

        Après essai, en essayant d'optimiser le m[i][j], il n'y a quasiment pas de différence. Je n'ai pas essayé en changeant le sens de la matrice, et j'imagine qu'il n'y a plus d'intérêt vu que la rapidité de indices tient à la manière dont le cache charge simultanément les lignes de la matrice.

        Donc je réitère, je te présente toutes mes excuses pour cet exercice qui est en fait assez intéressant quant au fonctionnement de la mémoire. Et donc logiquement, il ne m'en reste plus à présenter au C++, quel dommage !

  • # Comment lancer les tests en C++ sur son propre ordinateur sous Linux ?

    Posté par  (site web personnel, Mastodon) . Évalué à 2.

    Hello,

    Je ne connais à peu près rien au C++, mais j'aimerais lancer ces tests sur mon propre ordinateur. J'ai un système Linux sous la main avec les outils de dev installés et j'ai récupéré le code, mais là je ne sais pas quoi faire.

    Parce j'ai écrit une version Java du benchmark, à la fois pour tester le système de microbenchmark de Java (JMH), et pour voir quel différence j'avais avec la version C++.

    Or, sur les grosse matrices (10 000 x 10 000) je trouve un facteur 10 en faveur de Java, et reproductible, ce qui me semble franchement bizarre… du coup je voulais lancer la version C++ pour voir ce que ça donnait chez moi :)

    Benchmark                                      Mode  Cnt       Score   Error  Units
MatrixElementsSumBenchmark.bestRatings         avgt    2  270629.189          ns/op
MatrixElementsSumBenchmark.bestRatingsArray    avgt    2  141597.575          ns/op

    La connaissance libre : https://zestedesavoir.com

Suivre le flux des commentaires

Note : les commentaires appartiennent à celles et ceux qui les ont postés. Nous n’en sommes pas responsables.