Journal Simulation situation en Italie

Posté par  (site web personnel) . Licence CC By‑SA.
Étiquettes :
4
19
mar.
2020

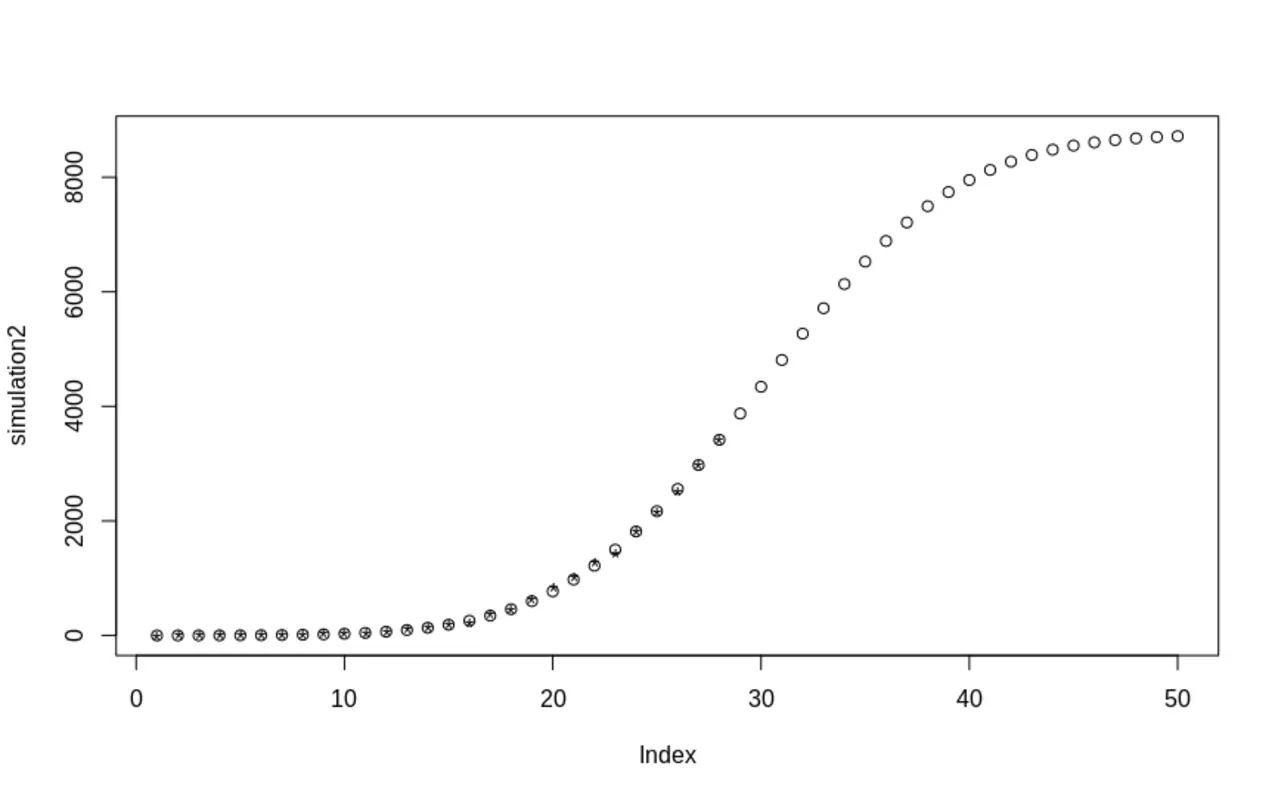
En jouant avec RStudio, j'ai pu retrouver la distribution du nombre de décès en Italie.

Nombre de décès en Italie

les ronds représentent la courbe théorique, les astérisques la courbe réelle.

pour obtenir ce résultat, j'ai simplement minimisé la variance entre les 2 courbes.

Ce que ça nous dit :

  • le pic de décès devrait être demain.
  • le nombre total de morts devrait être de 8717.

Voila…

  • # Et pour la France

    Posté par  . Évalué à 2.

    Et pour la France, ça donne quoi ?

    • [^] # Re: Et pour la France

      Posté par  (site web personnel) . Évalué à 2.

      Il y a l'Espagne qui m'intéresse en priorité. Je vais le faire pour la France après.

      • [^] # Re: Et pour la France

        Posté par  . Évalué à 3.

        Partageras-tu ton code sur github, gitlab ou n'importe ?

        • [^] # Re: Et pour la France

          Posté par  (site web personnel) . Évalué à 2.

          Il y a pas de code (enfin 1 ligne)…

          Pour l'Espagne, la distribution est :

          spain = c(1, 2, 8, 10, 17, 30, 36, 55, 86, 133, 196, 294, 342, 533, 638, 803)
           simulation2 = pnorm(1:30, mean = 20.12, sd = 5.09) * 1600 / 0.4

          plot(simulation2)
           points(spain, pch = "*")

          Il n'y a rien de plus… Je minimise à la main la variance :

          var(simulation2 - spain)
          C'est moins fiable pour l'Espagne. Si on trace la courbe, on obtient : 3896 morts, et un pic dans 4 jours.

        • [^] # Re: Et pour la France

          Posté par  (site web personnel) . Évalué à 3.

          J'ai mis le tout sur github :
          https://github.com/Taack/coronavirus

          • [^] # Tes résultats ne sont pas reproductibles

            Posté par  (site web personnel, Mastodon) . Évalué à 1.

            Je minimise à la main la variance

            À cause de ça, tes résultats ne sont pas (facilement, voire pas du tout) reproductibles. Comment une tierce personne est-elle supposée retrouver tes paramètres optimaux « à la main » ? Comment tenir une discussion sérieuse sur les résultats de la simulation si on ne peut pas facilement les répliquer ?

            Pourquoi ne pas utiliser une des fonctions d’optimisation inclues avec R ou d’un package tiers ? Avec ce modèle, pas trop de risque de tomber dans un optimum local, mais si c’est un problème le package minpack.LM est plus robuste que ce que propose R par défaut.

            • [^] # Re: Tes résultats ne sont pas reproductibles

              Posté par  (site web personnel) . Évalué à 1.

              Je connais pas bien RStudio, je l'utilise seulement depuis hier. Je relève le défi, je vais essayer de faire une fonction qui détermine les variables par dichotomie.

              Par contre, pour la version manuelle, j'ai d'abord utilisé le fichier ODS pour avoir une idée de ce que je cherchais… ça ne va pas être si simple de ne pas partir de n'importe quoi.

            • [^] # Re: Tes résultats ne sont pas reproductibles

              Posté par  (site web personnel) . Évalué à 1.

              J'ai ajouter dans github le code de convergence. Il ne se limite qu'a calculer les parties entières des paramètres.

              C'est crade, mais le voici :

              # d: dataset, m: mean, sd: width, a: aplitude

normApplitude <- function(d, m, sd) {
  d[length(d)] / pnorm(length(d):length(d), mean = m, sd = sd)
}

normVariance <- function(d, m, sd, a) {
  var(d - pnorm(1:length(d), mean = m, sd = sd) * a)
}

mTab = c(length(d):(length(d)+40))
sdTab = c(4:10)

print(mTab)
print(sdTab)
vOrig = Inf

aApprox = 0
mApprox = 0
sdApprox = 0

for (sd in sdTab) {
  for(m in mTab) {
    a = normApplitude(italy, m, sd)
    v = normVariance(italy, m, sd, a)
    if (v < vOrig) {
      sdApprox = sd
      mApprox = m
      aApprox = a
      vOrig = v
    }
  }
}

              il faut rentrer le tableau du nombre de morts "italy", puis sourcer le code.

              • [^] # Re: Tes résultats ne sont pas reproductibles

                Posté par  (site web personnel) . Évalué à 1.

                Version plus optimiste que la précédente et sans doute plus juste :

                # d: dataset, m: mean, sd: width, a: aplitude

normApplitude <- function(d, m, sd) {
  d[length(d)] / pnorm(length(d):length(d), mean = m, sd = sd)
}

normVariance <- function(d, m, sd, a) {
  var(d - pnorm(1:length(d), mean = m, sd = sd) * a)
}

mTab = c(length(d):(length(d)+40))
sdTab = c(4:10)

print(mTab)
print(sdTab)
vOrig = Inf

aApprox = 0
mApprox = 0
sdApprox = 0

for (a in c(5000:20000)) {
  for (sd in sdTab) {
    for(m in mTab) {
      v = normVariance(italy, m, sd, a)
      if (v < vOrig) {
        sdApprox = sd
        mApprox = m
        aApprox = a
        vOrig = v
      }
    }
  }
}

                Les résultats diffèrent un peu de ce que je trouve à la main … J'analyse et je fais un retours.

                • [^] # Re: Tes résultats ne sont pas reproductibles

                  Posté par  (site web personnel) . Évalué à 1.

                  Pour info, on trouve comme paramètres pour la courbe théorique avec le second algorithme de convergence :

                  amplitude = 9571 (c'est le nombre de morts total)
                  jours = 31 (ce n'est pas demain, mais après demain)
                  largeur de la gaussienne = 8

                  Je vais mettre ça sur github au propre.

                • [^] # Re: Tes résultats ne sont pas reproductibles

                  Posté par  . Évalué à 4.

                  Bonjour,

                  une proposition de code plus dans l'esprit de R (le langage c'est R, Rstudio n'est qu'un IDE pour R)

                  # d: dataset, m: mean, sd: width, a: aplitude

normApplitude <- function(d, m, sd) {
  d[length(d)] / pnorm(length(d):length(d), mean = m, sd = sd)
}

normVariance <- function(d, m, sd, a) {
  var(d - pnorm(1:length(d), mean = m, sd = sd) * a)
}

mTab = c(length(d):(length(d)+40))
sdTab = c(4:10)

print(mTab)
print(sdTab)

dta<-expand.grid(m=mTab,sd=sdTab,a=5000:20000)
dta$v=apply(dta,1,function(x) normVariance(d, x[1], x[2], x[3]))
dta[dta$v==min(dta$v),]

                  • [^] # Re: Tes résultats ne sont pas reproductibles

                    Posté par  (site web personnel) . Évalué à 1.

                    Merci, je l'adapterai sur git demain, en même temps que la mise à jour des résultats. Je vais essayer d'améliorer l'ajustement des paramètres pour des valeurs non entière, notamment sd.

                    Bonne soirée.

                    • [^] # Re: Tes résultats ne sont pas reproductibles

                      Posté par  (site web personnel, Mastodon) . Évalué à 2. Dernière modification le 20 mars 2020 à 20:23.

                      Je vais essayer d'améliorer l'ajustement des paramètres pour des valeurs non entière

                      Cela revient à réinventer la roue, ou plutôt de nombreuses roues qui tournent déjà très bien, car faire passer une ligne au plus près d’un ensemble de points c’est un truc que tous les scientifiques font régulièrement depuis des lustres.

                      Tu peux coder ton propre optimiseur si ça t’amuse (avec le confinement c’est pas le temps libre qui manque), mais si ce sont les résultats qui t’intéressent tu les obtiendras bien plus facilement en utilisant les fonctions d’optimisation à ta disposition dans R (la fonction nls) ou dans le package minpack.LM (la fonction nlsLM). Voilà une piste pour démarrer : https://www.r-bloggers.com/first-steps-with-non-linear-regression-in-r/

                      • [^] # Re: Tes résultats ne sont pas reproductibles

                        Posté par  (site web personnel) . Évalué à 1.

                        merci pour ce lien, je vais essayer d'utiliser ces outils.

                        Je pense qu'il faut aussi mettre en avant la variance, et l'incertitude qu'elle projette dans le résultat final. sachant qu'aujourd'hui la variance est de 800, elle doublera pour le résultat final.

                    • [^] # Re: Tes résultats ne sont pas reproductibles

                      Posté par  . Évalué à 4.

                      Une petite remarque complémentaire.
                      Avec R, une règle de conduite qui n'est pas absolue mais devrait l'être pour un débutant est : Jamais de boucle.
                      Il est (presque) toujours possible de s'en passer et comprendre comment s'en passer permet de progresser significativement dans l'apprentissage de ce langage, et ça permet de faire du code plus lisible.

                      Mes 2 centimes

  • # Quel modèle ?

    Posté par  . Évalué à 3.

    Quelle fonction a été utilisée comme modèle ? Une simple sigmoïde ? Et y a-t-il une raison particulière à ce choix ?

    • [^] # Re: Quel modèle ?

      Posté par  (site web personnel) . Évalué à 2. Dernière modification le 19 mars 2020 à 21:16.

      C'est simplement la distribution normal (c.f. précédant journal). La courbe est simplement :

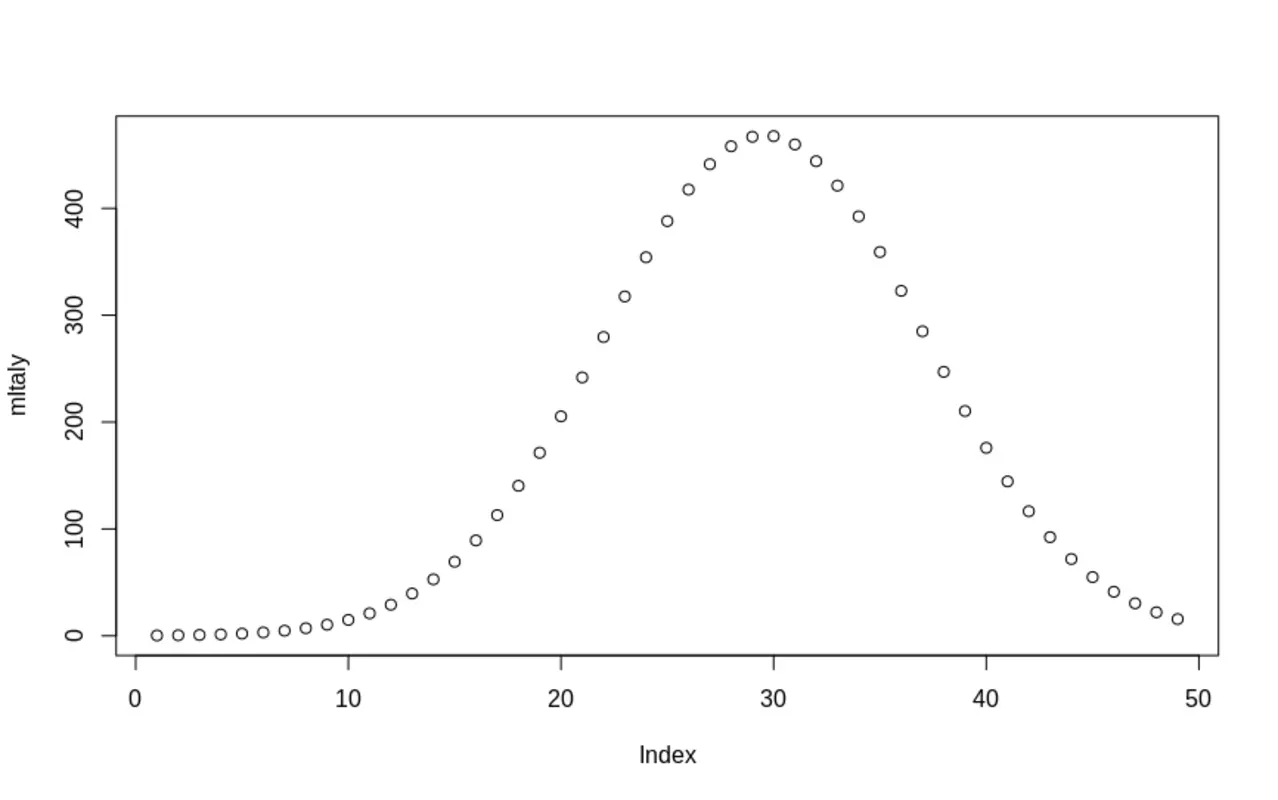
      pnorm(1:50, mean = 30.07, sd = 7.447) * 3500 / 0.4

      sa dérivé indique le nombre de mort par jours :

      d = c(-1, 1)
      mItaly = convolve(pnorm(1:50, mean = 30.07, sd = 7.447) * 3500 / 0.4, d, type = "filter")
      #M/J

  • # modèle

    Posté par  (site web personnel) . Évalué à 6.

    Et si tu essayais avec un polynome de degré 5. Ou une exponentielle ?

    Le point d'inflexion semble inventé par la sigmoïde.

    • [^] # Re: modèle

      Posté par  (site web personnel) . Évalué à 2.

      C'est l'intégrale d'une gaussienne centrée en LOG("POPULATION";PUISSANCE(2;1/2,5)).

      On part du principe comme évoqué dans le précédant journal que le virus :

      • à l'instant 0 multiplie par 2 le nombre d'infectés tous les 2,5 jours ;
      • au début des mesures de prévention, une part importante de la population est déjà infectée donc elles n'ont que très peu d'effets ;

      on peut établir que nombre d'infectés >> nombre de mort (c'est une très bonne nouvelle) et que la propagation s'apparente à la diffusion d'information au sein d'un mouvement brownien.

      • la vitesse de propagation du virus est proportionnelle au reste de la population à infecté, sur la population infectés (si 10 % infectés, le virus se propagera à 90 % de sa vitesse d'origine, et ainsi de suite) ;
      • le nombre de mort est proportionnel (quelque soit le nombre de lits d’hôpital) au nombre d'infectés décalé de plusieurs jours.

      Le moment ou la dérivé seconde du nombre d'infecté est nul (le fameux pic) est
      LOG(;PUISSANCE(2;1/2,5))

      • [^] # Re: modèle

        Posté par  (site web personnel) . Évalué à 2.

        On crée une série en respectant les principes ci-dessus, voilà ce que ça donne:

        Simu France Non Ajustée

        Un graphique vaut mieux qu'un long discourt, je résume la démarche théorique :

        Concernant le nombre d'infectés

        • Accélération du virus est une constante, dont la formule est Acc=PUISSANCE(2;1/2.5)
        • la "demie-vie" est =LOG(PopulationTotal;Acc)
        • le nombre d'infecté pour un jour est Fj=Fj-1+Fj-1*(Acc-1)*(1-RatioDesInfectés)
        • le ratio des infecté est RatioDesInfectés = =(Fj)/(PopulationTatal)

        Concernant le nombre de mort

        • on convolue le nombre d'infectés obtenu par une gaussienne centrée en 10 et de largeur 3.

        Je peux vous filer l'ODS si vous voulez … Dites moi comment faire pour l'envoyer..

      • [^] # Re: modèle

        Posté par  (site web personnel) . Évalué à 7.

        NON, les mesures de confinement, même prises trop tard comme en Italie, ont des effets très importants pour limiter le nombre de malades et surtout le nombre de morts.

        on peut établir que nombre d'infectés >> nombre de mort

        On est autour d'un taux de mortalité de 1% pour les malades tant que les hôpitaux ne sont pas débordés, et de 5% ensuite. C'est énorme et on voit l'importance de ne pas surcharger les hôpitaux. Les mesures de confinement sont super importantes pour ça. J'encourage tout le monde à suivre au mieux les recommandations des scientifiques sur les mesures de distanciation sociale.

        • [^] # Re: modèle

          Posté par  (site web personnel) . Évalué à 1.

          d'où tu sors ce taux de mortalité ??? le taux que je calcule est le même que la grippe (0,002). On a AUCUNE information sur ce taux, puisqu'il dépend du nombre total de porteurs sains qui n'est pas mesuré …

          Bien sûr que les hôpitaux ont une influence sur ce taux, mais ce n'est pas ce que je dis : La forme de la courbe ne dépend pas de ce taux … On peut donc facilement déterminer le moment où la courbe s'infléchie, qqs le nombre de lits.

          Pour l'Italie, ça semble être demain (j'ai mal lu le graphe lors de l'envoie) c.a.d. le 21 .. Pour l'Espagne et la France, la variance est encore trop importante. J'ai tout mis sur github.

          Pour les mesures de confinement, elles sont très importante en début d'épidémie. Une fois que 20 % de la population est infectée, elles permettent aussi de protéger les populations sensibles. Et les lits d’hôpitaux sont, bien sûr, très important pour limiter le nombre de mort. Tu vas sur un terrain où personne ne veut s'engager.

          • [^] # Re: modèle

            Posté par  . Évalué à 5. Dernière modification le 20 mars 2020 à 09:48.

            On a AUCUNE information sur ce taux, puisqu'il dépend du nombre total de porteurs sains qui n'est pas mesuré …

            On a les chiffres de la Corée du Sud qui a effectué un très grand nombre de tests y compris sur les personnes sans symptôme.

          • [^] # Re: modèle

            Posté par  (site web personnel) . Évalué à 5.

            Ces taux de mortalité viennent des études scientifiques. Par exemple, cette étude publiée chez Nature avance 1,4% : https://www.nature.com/articles/s41591-020-0822-7.

            On a AUCUNE information sur ce taux, puisqu'il dépend du nombre total de porteurs sains qui n'est pas mesuré …

            On n'a pas de mesure très précise mais on commence quand même à avoir une idée de l'ordre de grandeur. Il y a eu des cas où on a testé toute la population après une vague d'épidémie (paquebot de croisière mis en quarantaine, quelques petites villes italiennes pour lesquelles la vague est passée). L'ordre de grandeur, c'est environ 50% des contaminés ne vont pas développer de symptômes (et 50% des contaminations par une personne qui va développer des symptômes se fait avant l'apparition des symptômes => 75% des contaminations se fait par une personne qui ne présente pas de symptôme). Quand je parle de 50%, ça sera peut-être 30% ou 70%, mais en tout cas, ça paraît très peu probable qu'il y ait dix fois plus de contaminés sans symptômes.

            Bien sûr que les hôpitaux ont une influence sur ce taux, mais ce n'est pas ce que je dis : La forme de la courbe ne dépend pas de ce taux … On peut donc facilement déterminer le moment où la courbe s'infléchie, qqs le nombre de lits.

            La forme de la courbe dépend de R0, qui dépend des mesures de confinement. Et la courbe du nombre de malades ne dépend pas du nombre de lits. Le nombre de morts, par contre, dépend du nombre de malades et du nombre de lits. Et c'est très important de respecter les mesures de précaution pour limiter le nombre de malades, et surtout éviter de surcharger les hôpitaux.

            Une fois que 20 % de la population est infectée

            On est encore très très loin d'avoir 20% de la population infectée.

            • [^] # Re: modèle

              Posté par  (site web personnel) . Évalué à 1.

              Ces taux de mortalité viennent des études scientifiques. Par exemple, cette étude publiée chez Nature avance 1,4% : https://www.nature.com/articles/s41591-020-0822-7.

              L'article en question pose une simple division comme postulat…

              On n'a pas de mesure très précise mais on commence quand même à avoir une idée de l'ordre de grandeur. Il y a eu des cas où on a testé toute la population après une vague d'épidémie (paquebot de croisière mis en quarantaine, quelques petites villes italiennes pour lesquelles la vague est passée). L'ordre de grandeur, c'est environ 50% des contaminés ne vont pas développer de symptômes (et 50% des contaminations par une personne qui va développer des symptômes se fait avant l'apparition des symptômes => 75% des contaminations se fait par une personne qui ne présente pas de symptôme). Quand je parle de 50%, ça sera peut-être 30% ou 70%, mais en tout cas, ça paraît très peu probable qu'il y ait dix fois plus de contaminés sans symptômes.

              C'est très intéressant, seulement, il y a 3 "mais" :

              • les tests mettent 4 jours à donner des résultats, comment établir une vraie mesure dans ces conditions ?
              • Le virus à 2 souches, celle qui sévi en Europe est bien plus virulente que pour la Corée ou pour les confinés du paquebot.
              • Chloroquine a été massivement utilisée en Corée.

              La forme de la courbe dépend de R0, qui dépend des mesures de confinement. Et la courbe du nombre de malades ne dépend pas du nombre de lits. Le nombre de morts, par contre, dépend du nombre de malades et du nombre de lits. Et c'est très important de respecter les mesures de précaution pour limiter le nombre de malades, et surtout éviter de surcharger les hôpitaux.

              Oui, seulement je trouve cynique de parler de nombre de lits dans une simulation. Elle implique des décisions éthiques. Je ne veux pas parler d’hôpital, on verra à la fin qui avait la bonne stratégie.

              On est encore très très loin d'avoir 20% de la population infectée.

              On verra dans 2 jours.

              • [^] # Re: modèle

                Posté par  (site web personnel) . Évalué à 4.

                Le virus à 2 souches, celle qui sévi en Europe est bien plus virulente que pour la Corée ou pour les confinés du paquebot.

                Source ? Car cela semblait démenti jusqu'à présent.

                Oui, seulement je trouve cynique de parler de nombre de lits dans une simulation. Elle implique des décisions éthiques. Je ne veux pas parler d’hôpital, on verra à la fin qui avait la bonne stratégie.

                Je ne vois pas le rapport. Le but d'une simulation est d'essayer de coller au maximum à la réalité en tenant compte des facteurs connus et facilement reproductibles.

                On sait que si le nombre de patients ayant besoin d'assistance respiratoire dépasse les capacités hospitalières, le nombre de décès sera bien plus élevé qu'en temps normal.

                Donc un modèle un minimum crédible dépend de ce facteur de charge à un instant donné. C'est triste mais c'est la réalité des choses. Comme c'est une simulation, je ne vois pas l'implication éthique dedans qui incombera hélas uniquement à l'équipe soignante.

                • [^] # Re: modèle

                  Posté par  (site web personnel) . Évalué à 1.

                  Source ? Car cela semblait démenti jusqu'à présent.

                  https://academic.oup.com/nsr/advance-article/doi/10.1093/nsr/nwaa036/5775463

                  Si ceux qui démentent sont les mêmes qui émettent des réserves sur l'efficacité de la chloroquine …

                  Je ne vois pas le rapport. Le but d'une simulation est d'essayer de coller au maximum à la réalité en tenant compte des facteurs connus et facilement reproductibles.

                  On sait que si le nombre de patients ayant besoin d'assistance respiratoire dépasse les capacités hospitalières, le nombre de décès sera bien plus élevé qu'en temps normal.

                  Donc un modèle un minimum crédible dépend de ce facteur de charge à un instant donné. C'est triste mais c'est la réalité des choses. Comme c'est une simulation, je ne vois pas l'implication éthique dedans qui incombera hélas uniquement à l'équipe soignante.

                  Pour l'Italie, le nombre de lits est pas important pendant le pic. Donc ça ne change pas la date. Je ferais évoluer le modèle pour la France.

                  • [^] # Re: modèle

                    Posté par  (site web personnel) . Évalué à 7.

                    Si ceux qui démentent sont les mêmes qui émettent des réserves sur l'efficacité de la chloroquine …

                    Cela ne signifie pas qu'ils ont torts pour autant. Les études sur la chloroquine à ce sujet ne sont pas exempts de tout défaut non plus. Donc il convient d'être prudent surtout que l'urgence et la médiatisation pousse à la course à la découverte au détriment du respect des protocoles et des revues d'article efficaces.

                    Il faut donc se méfier des annonces révolutionnaires en cette épriode, non pas que la chloroquine n'est pas intéressante mais il ne suffit pas d'une annonce pour que cela fasse des miracles. Par ailleurs il semble aussi que ce traitement reste risqué car nécessite un dosage assez précis et pas anodin…

      • [^] # Re: modèle

        Posté par  . Évalué à 2.

        au début des mesures de prévention, une part importante de la population est déjà infectée donc elles n'ont que très peu d'effets ;

        Peux tu définir "une part importante", et expliquer pourquoi cela rend les mesures de prévention inutiles ?

        • [^] # Re: modèle

          Posté par  (site web personnel) . Évalué à 1.

          Si les symptômes du virus sont effectifs (désolé pour ce mot) après 10 jours, avec une variance de 5 jours (et pas 3 comme je l'ai marqué plus haut), on a la courbe "théorique" dans l'autre commentaire :

          https://linuxfr.org/nodes/119702/comments/1802877

          à partir du moment où on observe 1% de mort par rapport au nombre de mort final, le nombre d'infecté est du genre de 10%.

          Honnêtement, j'espère ne pas trop me tromper, car c'est un résultat optimiste.

  • # Prise en compte du confinement

    Posté par  . Évalué à 2.

    Si je ne m'abuse le confinement devrait avoir une influence en Italie et va commencer à montrer ses effets (un ralentissement de la propagation), le pic pourrait être retardé.

    Ce serait intéressant de voir si les astérisque vont plus bas que la courbe réel au cours du temps.

    • [^] # Re: Prise en compte du confinement

      Posté par  (site web personnel) . Évalué à 1.

      P-e, mais une grosse part de la population est déjà infectée, les mesures ont été bien trop tardive. Elles vont quand même p-e infléchir la courbe dans quelques jours.

      • [^] # Re: Prise en compte du confinement

        Posté par  (site web personnel) . Évalué à 3.

        une grosse part de la population est déjà infectée

        je ne dirai certainement pas que c'est faux, mais comment le sais tu? si on s'en tient au nombre de cas testés, il est faible par rapport à la population. Nous savons bien sûr que le nombre de cas réel est supérieur, mais pas de combien. 10x? 100x ?

        3 405 décès
        60 millions d'habitants.

        même s'il y a 1000 fois plus de cas que de décès, ça fait 3,4M de cas?

        • [^] # Re: Prise en compte du confinement

          Posté par  (site web personnel) . Évalué à -1.

          Dans notre entreprise, il y avait 6 cas suspectés lundi qui ont des symptômes. J'ai la gueule de bois, mais pas de fièvre (et je ne me compte pas. Un nombre substantiel de personnes toussait aussi). Il y a 80 personnes au total en France. Nous avons fermé et pris toutes les mesures nécessaires.

          Donc lundi, déjà dans mon entourage professionnel, une proportion non négligeable… ça vaut ce que ça vaut.

  • # Sources ?

    Posté par  . Évalué à 3.

    Quelles sont les sources pour les données théoriques ?

    Question théorie, s'il y a encore malade lorsque le confinement cesse, on repart pour un tour avec une courbe (quasiment) similaire, non ?

    • [^] # Re: Sources ?

      Posté par  . Évalué à 3.

      Oui : https://www.imperial.ac.uk/media/imperial-college/medicine/sph/ide/gida-fellowships/Imperial-College-COVID19-NPI-modelling-16-03-2020.pdf

    • [^] # Re: Sources ?

      Posté par  (site web personnel) . Évalué à 5.

      Après le but n'est pas d'avoir un confinement infini (car il est assez improbable que dans le monde entier il n'y ait plus de malades) ni de forcément lâcher le confinement en mode on revit comme avant du jour au lendemain.

      Le but du confinement est de donner un coup d'arrêt à la progression de la maladie. Pas forcément pour retomber à 0 malades. Quand la situation est plus calme, relancer progressivement les activités, tout en gardant certains réflexes ou limitations quelques temps.

      Ainsi une immunité de groupe se formera progressivement, évitant la surcharge des hôpitaux, tout en n'ayant pas un confinement d'une durée trop longue.

      Car sinon il suffit d'un malade dans le reste du monde pour que la machine soit relancée, et à ce stade ce n'est plus possible de retomber à 0 malade. Du moins sans vaccins efficace.

      • [^] # Re: Sources ?

        Posté par  . Évalué à 2.

        L'étude que j'ai cité ci-dessus (et qui est celle qui a fait changer d'avis le gouvernement anglais) parle des seuils à définir pour le relâchement partiel ou total du confinement et des seuils à définir pour le réenclencher. L'idée étant bien sûr de rester sous la saturation du système de santé tout en relançant l'économie périodiquement. Si des médicaments efficaces arrivent (Plaquenil, par exemple), on n'aura peut-être moins (ou pas du tout) besoin de périodes de confinement avant l'arrivée d'un vaccin.

    • [^] # Re: Sources ?

      Posté par  (site web personnel) . Évalué à 4.

      Question théorie, s'il y a encore malade lorsque le confinement cesse, on repart pour un tour avec une courbe (quasiment) similaire, non ?

      La question n'a rien de théorique, elle va vraiment se poser. Idéalement, on sera en position de tester très largement et de suivre l'exemple de la Corée du Sud.

      Je recommande la lecture de ce fil pour comprendre les différentes stratégies possibles : https://twitter.com/BallouxFrancois/status/1240624849879535618

  • # Analyse pour aujourd'hui

    Posté par  (site web personnel) . Évalué à 2.

    j'ai ajouter sur github la variance des résultats. Et j'ai ajusté par rapport aux derniers relevés, je vais continuer à le faire en gardant un historique.

    Tout va se jouer dans les prochains jours en Italie. J'espère que la situation ne va pas trop empirer.

    Pour la France, il y a un grand plateau, ce qui est rassurant, et peut s'expliquer par le fait que le virus a été virulent d'abord dans le "Grand Est", puis est allé sur Paris, avec un certains décalage. Puis enfin, les mesures de confinement.

    Bien sûr, ces courbes ne connaissent pas la géographie, ou les mesures politiques.

    Elle pourrait cependant être intéressante si la progression du virus est de > à 2 pour 2.5 jours. Car, dans ce cas, l'effet du confinement est moins visible (grande partie de la population infectée, difficile à contrôler). Si une grande partie de la population est infectée, l'année prochaine, le virus devrait avoir beaucoup plus de mal pour se propager, et sa létalité serait moins forte.

    Après, il y a la capacité et l'efficacité des hôpitaux qui croissent dans le temps, mais peuvent se trouver en sur-capacité.

    Un dernier mot concernant les tests : ils ne détectent que les porteurs du virus, on ne détecte pas ceux qui ont eu le virus. Donc très difficile d'estimer la population totale par extrapolation à partir des tests.

  • # A posteriori

    Posté par  (site web personnel) . Évalué à 2.

    le pic de décès devrait être demain.

    Malheureusement pas encore : https://fr.wikipedia.org/wiki/Pand%C3%A9mie_de_maladie_%C3%A0_coronavirus_de_2020_en_Italie#Chiffres_et_statistiques

    Les prédictions c'est difficile, surtout quand ça concerne le futur. :)

    Adhérer à l'April, ça vous tente ?

    • [^] # Re: A posteriori

      Posté par  (site web personnel) . Évalué à 1.

      Surtout quand on lit mal son propre graphique et qu'on minimise à la main … J'aurais au moins dû mettre la variance.

      Pour info, j'utilise maintenant l’algorithme conseillé venant du package minpack.lm, ça donne des résultats plus précis.

      Autant pour l'Espagne la date semble ne pas trop bouger (entre le 28,5 et le 29,5) d'un jour sur l'autre, autant pour l'Italie, ça a glissé énormément … J'essaie de minimiser en moyennant les prédictions sur les derniers jours. ça permet de lisser des cas de saturation des hôpitaux et ça donne une date un peu plus stable (entre le 23 et le 24).

      J'attends la semaine prochaine pour la France et les US.

      • [^] # Re: A posteriori

        Posté par  (site web personnel) . Évalué à 3.

        Si tu utilises toujours la loi normale, perso je ne suis pas très optimiste sur ce qu'on peut faire dire à ce genre d'identification, parce que ça considère en creux que les conditions de démarrage de l'épidémie sont les mêmes que celles à l'arrivée.

        Hors ce n'est manifestement pas le cas. Pour caricaturer, au début l'épidémie évolue dans un environnement naïf extrêmement vulnérable, et, passé un seuil de prise de conscience, elle évolue dans un contexte cloisonné. Donc la nature cette caricature serait plutôt une évolution franchement asymétrique, ce que ne représente pas ta courbe en cloche.

        Et si on veut sortir de la caricature pour faire des prédictions, il faudrait à mon sens enrichir un des modèles dynamiques tels que ceux présenté dans d'autres journaux (SIR ou SEIQR) avec une composante de distanciation sociale qui serait elle même fonction de la place de l'épidémie dans la population (prise de conscience des morts passés et en cours, probabilité de connaître un malade ou un mort, réglementation/réaction politique et économique, …). Ça n'a pas besoin d'être extrêmement complexe (peut être que juste la probabilité de connaître un mort est un facteur qui change fortement l'envie de suivre les consignes), mais éventuellement ce paramètre aurait une dépendance à d'autres systèmes dynamiques qui n'ont rien à voir de prime abord (simulant la dynamique de l'appareil médiatico politique, et/ou de l'appareil productif).

        Adhérer à l'April, ça vous tente ?

      • [^] # Re: A posteriori

        Posté par  (site web personnel) . Évalué à 3.

        Par curiosité, est-ce que tu as comparé tes prédictions avec ce que l'on connaît maintenant de la pandémie ?

        • [^] # Re: A posteriori

          Posté par  (site web personnel) . Évalué à 2.

          Le pic était annoncé prématurément.
          https://fr.wikipedia.org/wiki/Pand%C3%A9mie_de_Covid-19_en_Italie#Chiffres_et_statistiques

          Avec du recul on voit que le pic était le 27 mars (6 jours après) et que les valeurs entre temps étaient bien élevées.

          Adhérer à l'April, ça vous tente ?

          • [^] # Re: A posteriori

            Posté par  (site web personnel) . Évalué à 3.

            J'ai également l'impression que le choix d'une courbe en S, avec une accélération et une décélération de même vitesse était un mauvais choix à posteriori. Sur le graphique, on voit que ça a grimpé très rapidement (exponentielle) mais que la descente est bien plus lente (linéaire ?).

            • [^] # Re: A posteriori

              Posté par  (site web personnel) . Évalué à 4.

              La courbe en S est le bon modèle quand tu es en mode on ne fait rien où la seule limite pour propager le virus est de trouver de nouveaux malades potentiels, donc non infectés par le passé.

              Après pour modéliser les mesures d'un confinement, il ne fonctionne pas, car il faudrait modéliser proprement l'impact réel du confinement mis en place ce qui n'est pas évident du tout et très variable d'un pays à l'autre.

Suivre le flux des commentaires

Note : les commentaires appartiennent à celles et ceux qui les ont postés. Nous n’en sommes pas responsables.